愛知医科大学物理2013年第3問

問1.次の文中の$\fbox{1}$~$\fbox{4}$にあてはまる式を答えよ。ただし、コンデンサーは真空中にあり、コンデンサーの端の影響は無視できるとする。

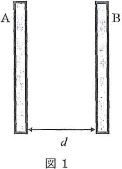
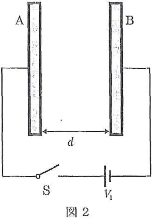
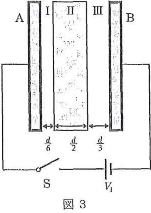
図1のように、面積$S$[m²]の帯電していない極板$\text{A}$、$\text{B}$を距離$d$ [m]だけ離して平行に置いたコンデンサーがある。真空の誘電率を$\epsilon_0$[C²/(Nm²)]とすると、コンデンサーの静電容量は$\fbox{1}$[F]となる。コンデンサーの極板間に電位差$V$ [V]を与えると、蓄えられる電荷は$\fbox{2}$[C]となり、このときの極板間の電場(電界)の強さは$\fbox{3}$[N/C]となる。極板間の電場の強さを$E$ [N/C]としたとき、$\fbox{2}$、$\fbox{3}$を用いて蓄えられる電荷を、$S$、$\epsilon_0$、$E$を用いて表すと$\fbox{4}$[C]となる。

ここで電気力線について考える。電気力線は目に見えない電場の様子を表すのに用いられる。電場の強さは電気力線の密度に比例し、電場の強さが$E$ [N/C]の位置では、電場に垂直な断面を通る電気力線の密度を$E$[本/m²]とする。電荷と$\fbox{4}$の関係から、$Q$ [C]の電荷が蓄えられたコンデンサーの極板間の電気力線の本数は$\dfrac{Q}{\epsilon_0}$ [本]となる。
問2.図1のコンデンサーに電圧$V_1$の直流電源とスイッチ$\text{S}$をつなぎ、図2のようにしてスイッチを閉じた。十分時間が経過した後、コンデンサーに蓄えられた電荷は$Q_1$であった。
- (1)次の場合の極板間の電気力線の本数を、$\epsilon_0$、$Q_1$、$V_1$の中から必要なものを用いて表せ。
  - (a)スイッチを開いた場合(極板間の距離は$d$)
  - (b)スイッチを開いてから、極板間の距離を$d$から$2d$にした場合
  - (c)スイッチを閉じたまま、極板間の距離を$d$から$2d$にした場合
- (2)次の場合のコンデンサーに蓄えられるエネルギーを、$\epsilon_0$、$Q_1$、$V_1$の中から必要なものを用いて表せ。
  - (a)スイッチを開いた場合(極板間の距離は$d$)
  - (b)スイッチを開いてから、極板間の距離を$d$から$2d$にした場合
  - (c)スイッチを閉じたまま、極板間の距離を$d$から$2d$にした場合
問3.図2の状態でスイッチ$\text{S}$を閉じて、コンデンサーに蓄えられた電荷が$Q_1$になってからスイッチを開いた。そして図3のように、極板間に極板と同じ面積で厚さ$\dfrac{d}{2}$の帯電していない平らな導体を、極板Aから$\dfrac{d}{6}$だけ離して平行に挿入した。極板AB間の領域を、左からそれぞれI(極板Aと導体の間)、II(導体内部)、III(導体と極板Bの間)とする。
- (1)領域I~IIIの電気力線の本数を、$S$、$d$、$\epsilon_0$、$Q_1$の中から必要なものを用いてそれぞれ表せ。
- (2)コンデンサー全体に蓄えられるエネルギーを、$S$、$d$、$\epsilon_0$、$Q_1$の中から必要なものを用いて表せ。
問4.図3の状態から、挿入した導体を、極板と平行に保ちながら極板Aから$\dfrac{d}{3}$だけ離れた位置までゆっくりと右に移動させた。このとき、次の量は導体の移動中にどのように変化したか、下の(ア)~(オ)の中から1つ選び、記号で答えよ。
- (1) 領域Iにおける電気力線の本数
- (2) コンデンサー全体に蓄えられるエネルギー
- (ア) 増加した
- (イ) 増加した後減少した
- (ウ) 変化しない
- (エ) 減少した
- (オ) 減少した後増加した