2重スリットによる光の干渉実験について考える。図1のように単スリット$\text{S}$をもつ板$\text{F}$と2重スリット$\text{AB}$をもつ板$\text{G}$およびスクリーンを平行に配置して、単スリット$\text{S}$の左側から位相がそろった波長$\lambda$の単色光を入射させる。スリット$\text{A}$、$\text{B}$の間隔を$2d$、板$\text{F}$と板$\text{G}$との距離を$h$、板$\text{G}$とスクリーンとの距離を$L$とする。点$\text{O}$は$\text{AB}$の垂直二等分線がスクリーンと交わる点である。点$\text{O}$から$y$だけ離れたスクリーン上の点を点$\text{P}$とする。以下の問において、$d$と$y$は$L$と$h$より十分に小さいものとして近似せよ。また、空気の屈折率は1としてよい。はじめ、単スリット$\text{S}$は$\text{AB}$の垂直二等分線上にあるとする。

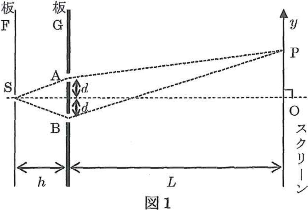
• 問1 点$\text{P}$に点$\text{O}$から数えて$m$番目の暗線ができるとき、$\lambda$を$m$、$d$、$L$、$y$を用いて表せ。ここで、$m=1,2,3,\cdots$である。

次に、図2のように、半径$R$の半円柱形をした屈折率$n(n\gt 1)$のガラスを、半円柱の軸がスリット$\text{A}$の中心に一致するようにスリット$\text{A}$にかぶせる。半径$R$は$d$より小さいものとする。

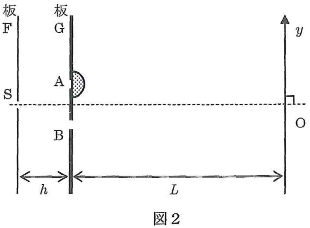
• 問2 ガラス中の光の波長はいくらか。
• 問3 ガラスをかぶせる前にスクリーン上の点$\text{O}$にあった最も明るい明線は、ガラスをかぶせた後、$y$軸の正負どちら側にどれだけ移動するか。正負については解答欄で正しい方に$\circ$をつけよ。

次に半円柱形のガラスをスリット$\text{A}$にかぶせた状態のまま、単スリット$\text{S}$の位置を$y$方向に移動させたところ、最も明るい明線の位置が点$\text{O}$に戻った。

• 問4 このとき、単スリット$\text{S}$を$y$方向の正負どちら側にどれだけ移動させたか。正負については解答欄で正しい方に$\circ$をつけよ。

次に図1の状態に戻してから、図3のように板$\text{G}$とスクリーンの間の上半分の領域を屈折率$n$の物質で満たす。スクリーン上に点$\text{O}$を挟んで点$\text{O}$から等距離に点$\text{Q}_1$、点$\text{Q}_2$をとる。

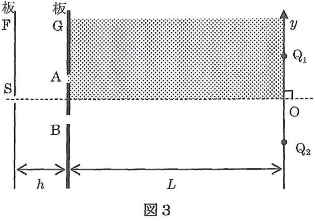
• 問5 単スリット$\text{S}$から点$\text{Q}$に至る光路$\text{S}→\text{A}→\text{Q}_1$と$\text{S}→\text{B}→\text{Q}_1$、および、点$\text{Q}_2$に至る光路$\text{S}→\text{A}→\text{Q}_2$と$\text{S}→\text{B}→\text{Q}_2$を解答欄の図中に示せ。