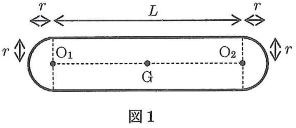
図1のような形状をした棒がある。この棒の両端は半径$r$の半球形で、その間の部分は断面が半径$r$、長さ$L$の円柱形になっている。この棒は一様で重心$\text{G}$は棒の中心にある。また、棒の質量を$m$とする。図1中の点$\text{O}_1$と点$\text{O}_2$は各々両端の半球の中心である。

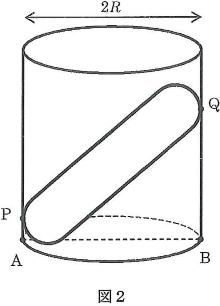
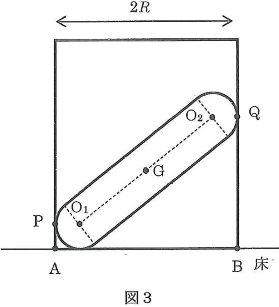
いま、図2のように、断面の半径が$R$の円筒を水平な床の上に置き、棒をこの円筒に静かに入れたところ静止した。図中の点$\text{P}$と点$\text{Q}$は棒と円筒内壁との接点である。また、円筒には底が無いので棒の下点は床と接している。図2で$\text{AB}$は円筒の直径で、点$\text{P}$は点$\text{A}$の、点$\text{Q}$は点$\text{B}$の真上にある。図3は円筒に入れた棒を真横から見た図である。床と円筒、床と棒、円筒と棒の各々の間に摩擦はなく、円筒の重心は円筒の中心軸上にあるものとする。

尚、$0\lt R-r\lt L/2$であり、重力加速度の大きさを$g$として以下の問に答えよ。

• 問1 点$\text{Q}$で棒が円筒から受ける垂直抗力$N_Q$を求めよ。
• 問2 円筒と棒が静止したことから、円筒の質量$M$は棒の質量$m$の何倍以上であると考えられるか、$R$、$r$を用いて表すこと。 解答欄には最後の結果だけでなく途中の考えも書くこと。
• 問3 半径の比が$r/R=1/2$、質量の比が$M/m=1/4$であるとき、静かに棒を入れても円筒は倒れる。いま、点$\text{O}_1$に電荷$-q$の点電荷を、点$\text{O}_2$に電荷$+q$の点電荷を固定したとしよう$(q\gt 0)$。外部から水平方向に大きさ$E$の一樣電場をかけて円筒および棒を静止させるためには、電場を図3の左右どちら向きにかければよいか。解答欄で正しい方を〇で囲め。また、その電場の大きさ$E$をいくら以上にする必要があるか、$M$、$g$、$q$、$R$、$L$を用いて答えよ。ただし、点電荷の質量は無視できるものとする。