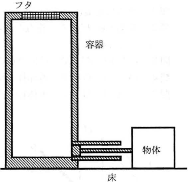
大気圧$P_0$[Pa]の室内に図のような装置を用意する。内側の高さ$H$[m]、容積$V$[m³]の容器の下部に断面積$A$[m²]のピストンが付いていて、ピストンは外側に置かれた質量$M$[kg]の物体と軽くて丈夫な棒でつながっている。ピストンの棒につながった面は大気に接している。容器は床に固定されていて、ピストンは摩擦なくなめらかに動く。一方、物体と床との間には摩擦がある。物体と床との間の静止摩擦係数を$\mu$、重力加速度を$g$[m/s²]とする。容器上部にはフタがあり、容器内の気体や水などを入れ換えることができる。このフタを閉めると完全に密閉することができる。また、容器の熱容量は無視でき、容器と外部との熱の出入りはなく、容器内の気体を加熱できるように作られている。水の密度を$\rho$[kg/m³]とし、水の密度の温度変化は無視できるものとする。

• 問1 容器上部のフタを開け水を注入し容器の中を水で満たしたとき、物体がピストンから受ける力の大きさを求めよ。ただし、物体は動かなかったとする。

次に、容器から水を全て抜き、容器の中を圧力$P_0$[Pa]、温度$T_0$[K]の気体で満たした後、フタをしてから加熱する。ただし、この気体は理想気体とみなせるものとする。気体定数を$R~[\text{J}/(\text{K}\cdot\text{mol})]$、気体の定積モル比熱を$\dfrac{3}{2}R~[\text{J}/(\text{K}\cdot\text{mol})]$として、以下の問に答えよ。

• 問2 気体の温度が$T_1$[K]より高くなったときピストンが動いた。この$T_1$を$P_0$、$T_0$、$M$、$A$、$g$、$\mu$を用いて表せ。
• 問3 気体の温度を$T_1$[K]にするために気体に加えた熱量$Q~[\text{J}]$を$M$、$A$、$V$、$g$、$\mu$を用いて表せ。

次に、ピストンと物体をもとの位置に戻してから容器に深さ$h$[m]$(h{\lt}H)$まで熱湯（$T_0$[K]より高温だが沸点より低い温度の水）を入れる。容器内の残りの部分は前問と同じ種類の気体で満たしてフタをする。ただし、熱湯の蒸発は無視でき、熱湯を入れた直後の気体の圧力を$P_0$[Pa]、温度を$T_0$[K]とする。

• 問4 気体の温度が上昇し、$T_2$[K]より高くなったときピストンが動いた。$(T_1-T_2)$を求めよ。