次の文章を読み、設問(1)～(4)に答えよ。設問(3)-(i)、(4)の解答は有効数字2桁で表し、計算の過程も示すこと。ただし、$[\text{A}]$は化合物$\text{A}$のモル濃度(mol/L)を表し、アボガドロ定数は$6.0\times10^{23}$/molとする。

高温で水素（気体）とヨウ素（気体）からヨウ化水素（気体）が生じる反応の反応速度を考えてみよう。

$$\text{H}_2+\text{I}_2\rightarrow2\text{HI}\tag{A}\label{aa}$$

反応がおこるためにはまず反応物どうしが衝突することが必要である。単位時間内に両分子が衝突する回数$Z$はそれぞれのモル濃度に比例するので、次の関係式が得られる。

$$Z=a\times[\text{H}_2]\times[\text{I}_2]（aは比例定数）\tag{B}\label{ab}$$

$\underline{a}$の値は温度が上昇すると大きくなる。

しかし、分子が衝突しても必ず反応がおこるわけではない。全衝突回数に対して反応のおこる割合を$b$とおくと、反応速度$v$と$Z$の間には次式の関係がある。

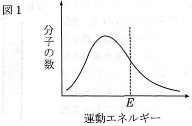
$$v=b{\times}Z（bは比例定数）\tag{C}\label{ac}$$

図1はある温度における気体分子の運動エネルギーの分布を表し、$E$はこの反応の活性化エネルギーに相当する。$\eqref{ac}$式の$b$の値も温度が上昇すると大きくなるが、これは温度の上昇により図1の$E$よりも大きい運動エネルギーを持った分子の数が増えて、分子が衝突したときに活性化状態になる分子の数が増大するからである。なお、反応$\eqref{aa}$の$E$の値は$174\text{kJ}/\text{mol}$である。

$\eqref{ab}$式と$\eqref{ac}$式より$\eqref{ad}$式が得られる。

$$v=k\times[\text{H}_2]\times[\text{I}_2]\tag{D}\label{ad}$$

$\eqref{ad}$式を反応速度式、$k$を反応速度定数という。

また、反応$\eqref{aa}$で生成したヨウ化水素分子どうしが衝突するとヨウ素と水素が生成する。

$$2\text{HI}\rightarrow\text{H}_2+\text{I}_2\tag{E}\label{ae}$$

反応$\eqref{ae}$の$E$（図1）の値は$183\text{kJ}/\text{mol}$である。

設問

• (1) 下線部の理由を説明せよ。
• (2) 次の(i)、(ii)の場合、図1の気体分子の運動エネルギーの分布と$E$はどのように変化するか、解答欄のグラフに模式的な図を書きこめ。変化しない場合は「変化なし」と記すこと。
  • (i) 容器の温度を下げた。
  • (i) 容器に触媒を添加した。

• (3) 容積一定の容器に、$3.0\times10^{24}$個の水素分子と$3.3\times10^{24}$個のヨウ素分子を入れて、700Kに保った。十分に時間をかけて反応で発生した熱を測定したところ$36\text{kJ}$であった。
  • (i) 反応$\eqref{aa}$と$\eqref{ae}$は互いに可逆反応である。反応$\eqref{aa}$を正反応とするときの700Kにおける平衡定数を求めよ。
  • (ii) 反応$\eqref{aa}$を正反応とするときの$T$(K)における平衡定数は36である。$T$(K)と700Kの関係はどうなるか、次の中から選び、記号で答えよ。また、その理由を説明せよ。
    • a. $T\lt700$
    • b. $T=700$
    • c. $T\gt700$
• (4) 700Kで1Lの容器に$6.0\times10^{20}$個のヨウ化水素分子が存在するとき、ヨウ化水素どうしの衝突回数は1秒間に$3.6\times10^{30}$回であり、$1.0\times10^{16}$回の衝突につき1回の割合で水素とヨウ素が生成すると仮定する。
  • (i) このときの反応速度を1秒間のヨウ素濃度の変化量(mol/(L・s))で表せ。
  • (ii) 反応$\eqref{ae}$の反応速度定数を求めよ。