次の設問(1)~(5)に答えよ。計算問題は、導出過程も簡潔にまとめて記し、解答は解答欄に記すこと。

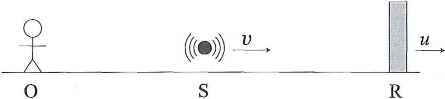
• (1) 図のように、一直線上に、静止している観測者$\text{O}$、振動数$f$の音を出す音源$\text{S}$、音をよく反射する反射壁$\text{R}$が並んでいる。音源$\text{S}$は一定の速さ$v$で一直線上を反射壁$\text{R}$のほうに向かって運動している。反射壁$\text{R}$も音源$\text{S}$と同じ方向に、一定の速さ$u$で運動している。音源$\text{S}$から出た音が反射壁$\text{R}$で反射して観測者$\text{O}$に達するとき、観測される音の振動数はいくらか。ただし、音速を$V(V\gt v、V\gt u)$とし、風はないものとする。
  
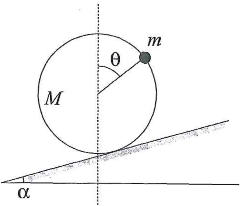
• (2) 図のように、質量$M$の一様な薄い円板の周上に大きさの無視できる質量$m$のおもりを固定し、この円板を傾斜角$\alpha$のあらい斜面上に、円板面が鉛直軸と斜面の最大傾斜方向の線を含む面内にあるように立てたところ、静止した。円板の中心とおもりとを結ぶ直線の鉛直線に対する角を$\theta$としたとき、$\sin\theta$の値を求めよ。
  
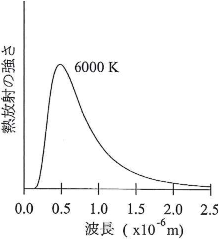
• (3) 有限の温度にある物体は、必ず電磁波を熱放射している。右図は、温度$6000$Kでの熱放射の強さを、波長の関数としてグラフにしたものである。解答用紙の図中($6000$Kでの熱放射の波長分布が薄く示されている)に、温度$5000$Kでの熱放射の強さの波長分布を実線で、温度$4000$Kでの熱放射の強さの波長分布を点線で、それぞれ概形を書き込め。
  
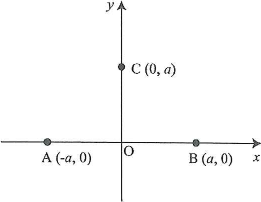
• (4) 真空中において、図のような$xy$座標軸をとり、点$\text{A}(-a,~0)$と点$\text{B}(a,~0)$に大きさ$q$の正の電荷を固定し、点$\text{C}(0,~a)$に負の電荷$-e$を持つ電子を置く。はじめ点$\text{C}$で静止していた電子が、電場から力を受けて$y$軸上を動くとき、原点$\text{O}$での速さを求めよ。ただし、真空中の電気に関するクーロンの法則の比例定数を$k$、電子の質量を$m$とする。
  
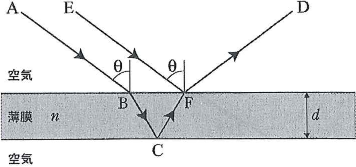
• (5) 図のように、単色光で位相のそろった平面波を、絶対屈折率1の空気中からある媒質の薄膜に入射角$\theta$で斜めに入射させた。$\text{A}$点から薄膜中を通って空気との間で反射した光$\text{ABCFD}$と、$\text{E}$点から薄膜の表面で反射した光$\text{EFD}$が$\text{D}$点において強め合うときの最長の波長を$\lambda_0$、2番目に長い波長を$\lambda_1$とするとき、その差$\lambda_0-\lambda_l$を求めよ。ただし、薄膜の厚さを$d$、薄膜の絶対屈折率を$n(\gt 1)$とする。