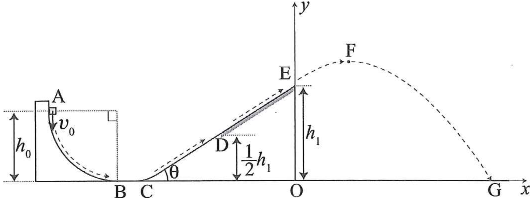
図のように、高さ$h_0$の地点から半径$h_0$の円弧(中心角が$90^\circ$)状の斜面$\text{AB}$が点$\text{B}$で水平な面に接するように固定されている。また、水平な面に対して角度$\theta(0^\circ\lt\theta\lt 90^\circ)$をなす斜面$\text{CE}$は、点$\text{C}$で水平な面になめらかに接続されている。円弧状の斜面出、水平な面$\text{BC}$および斜面$\text{CD}$はなめらかな面であり、斜面$\text{DE}$はあらい面である。小物体と斜面$\text{DE}$との間の動摩擦係数を$\mu '$、重力加速度の大きさを$g$とし、空気の抵抗は無視するものとする。水平な面から点$\text{D}$および点$\text{E}$までの高さを、それぞれ$\dfrac{1}{2}h_1$および$h_1$とし、$\dfrac{1}{2}h_1\lt h_0\lt h_1$とする。また、点$\text{E}$から水平面に垂線を下ろし、その交点を座標の原点$\text{O}$とし、座標軸は水平右向きに$x$軸、鉛直上向きに$y$軸をとる。次の各問いに答えよ。計算問題は、導出過程も簡潔にまとめて記し、解答は解答欄に記すこと。

• I.はじめに、円弧状の斜面上の点$\text{A}$から、質量が$m$で大きさの無視できる小物体を速さ$v_0$で滑り落とす。小物体は、円弧状の斜面$\text{AB}$を滑り落ちた後、点$\text{B}$をある速さで通過した。
  • (1) 小物体が点$\text{B}$を通過するときの速さを、$v_0$を用いた式で表せ。
• II.
  • (2) で求めた小物体が点$\text{B}$を通過するときの速さを$v_1$とする。点$\text{B}$を通過した小物体は、なめらかな斜面$\text{CD}$を上がり、点$\text{D}$をある速さで通過した。
  • (3) 小物体が点$\text{C}$から$\text{D}$まで上がったとき、小物体の位置エネルギーの増加量を求めよ。
  • (4) 小物体が点$\text{D}$を通過するときの速さを、$v_1$を用いた式で表せ。
• III.
  • (5) で求めた小物体が点$\text{D}$を通過するときの速さを$v_2$とする。点$\text{D}$を通過した小物体は、あらい斜面$\text{DE}$を上がり、点$\text{E}$から斜面$\text{DE}$に沿った方向にある速さで飛び出した。
  • (6) 小物体が斜面$\text{DE}$を上がるとき、小物体が斜面から受ける動摩擦力の大きさを求めよ。
  • (7) 小物体が$\text{DE}$間を通過するのにかかる時間を、$v_2$を用いた式で表せ。
  • (8) 小物体が点$\text{D}$から点$\text{E}$まで上がったとき、動摩擦力が小物体にした仕事の大きさ(絶対値)$W(W\gt 0)$を求めよ。
  • (9) 小物体が点$\text{E}$から斜面$\text{DE}$に沿った方向に飛び出す速さを、$v_1$および$W$を用いた式で表せ。
  • (10) 小物体が点$\text{E}$から斜面$\text{DE}$に沿った方向に飛び出すために$v_0$が満たすべき条件を、$W$を用いた式で表せ。
• IV.
  • (11) で求めた小物体が、点$\text{E}$から斜面$\text{DE}$に沿って飛び出すときの速さを$v_3$とする。その後、小物体は、点$\text{E}$から飛び出し、最高点$\text{F}$に達した後、水平な面上の点$\text{G}$に落ちた。
  • (12) 小物体が点$\text{E}$から斜面$\text{DE}$に沿った方向に飛び出したとき、小物体が達する最高点$\text{F}$の座標$(x_F,y_F)$を、$v_3$を用いた式で表せ。
  • (13) 小物体が飛び出した後、水平な面$\text{OG}$に最初に到達する点の$x$座標を、$v_3$を用いた式で表せ。