図に示すように、水平面に対して傾き30°の斜面と、その下端Pからなめらかに連続する水平な床がある。水平な床の右端Qには壁があり、PQ間の距離は$2l$、PQの中点を0とする。最初、質量$m$の小さな物体Aが斜面上の高さ$h$のところに、質量$M$の小さな物体BがOに静止していた。$x$軸を図のようにとり、Oを原点とし、$h{\lt}l$が成り立っているものとする。また、物体と斜面および床との摩擦は無いものとし、空気抵抗も無視できるものとする。重力加速度を$g$とし、符号に注意して以下の問いに答えよ。計算問題は、導出過程も簡潔にまとめて記し、解答は解答欄に記すこと。

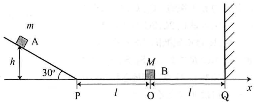
• $\text{I}.$ 物体Aは斜面上をすべり落ち、物体Bにはねかえり係数$e~(0{\lt}e{\lt}1)$で衝突した。
  • (1) 物体Aが点Pに到達するまでの時間を求めよ。
  • (2) 物体Aが点Pに到達してから、物体Bに到達するまでの時間を求めよ。
  • (3) 物体Aが物体Bに衝突する直前の物体Aの速度を求めよ。
  • (4) 衝突後の物体Aの速度を求めよ。
  • (5) 衝突後の物体Bの速度を求めよ。
• $\text{I}\hspace{-.1em}\text{I}.$ 物体Bの質量が、物体Aの質量の5倍である場合$(M=5m)$を考えよう。はねかえり係数$e=0.5$のとき、最初の衝突後、物体Aは$x$軸の負の方向に進み、斜面を点Rまでのぼり、再びすべり落ちた。
  • (6) 点Rの高さを求めよ。
  • (7) 物体Aが、物体Bに衝突してから点Rに達するまでにかかる時間を求めよ。
• $\text{I}\hspace{-.1em}\text{I}\hspace{-.1em}\text{I}.$ 次に、物体Bが、$x$軸の正の方向に進み、点Qで壁に完全弾性衝突する場合を考える。ただし、$h{\lt}l$の場合、物体Aが斜面をすべり下りて再び物体Bに衝突するのは、斜面上ではなく、水平な床PQ上である。
  • (8) 物体Aが斜面上で点Rに達してから、物体Aと物体Bが2回目に衝突するまでの時間を求めよ。
  • (9) 物体Aと物体Bの2回目の衝突がおこる位置の$x$座標を求めよ。
• $\text{I}\hspace{-.1em}\text{V}.$ 最後に、$\text{I}\hspace{-.1em}\text{I}\hspace{-.1em}\text{I}$の場合とは異なり、物体Bが$x$軸の正の方向に進み、点Qで壁にはねかえり係数$e'~(0{\lt}e'{\lt}1)$で非弾性衝突する場合を考える。
  • (10) 物体Aと物体Bの2回目の衝突が原点Oでおこる場合、はねかえり係数$e'$を求めよ。