図1のように、長さ$l$、断面積$S$、質量$M$のまっすぐで一様な金属線が水平に置かれ、その両端に可変抵抗器と起電力$V$の電池が導線で接続されている。*1金属線内の由自由電子は、電場から受ける力による加速と、熱振動する陽イオンなどとの衝突による減速とを繰り返しながら移動する。金属線の単位体積中の自由電子の数を$n$、電気素量を$e$として、次の各問いに答えよ。ただし、電流による金属線の温度上昇および電池の内部抵抗と導線の抵抗は無視できるものとする。計算問題は、導出過程も簡潔にまとめて記し、解答は解答欄に記すこと。

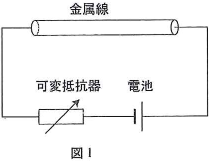
• I.はじめに、可変抵抗器の抵抗値を$R_1$としたところ、金属線を流れる電流の大きさは$I$であった。
  • (1) 金属線の両端に加わる電圧はいくらか。$I$を含んだ式で表せ。
  • (2) 金属線の中で、電場が一様であるとすると、電場の大きさはいくらか。Iを含んだ式で表せ。
• II.問題文での下線部*1について考えよう。簡単のために、自由電子はすべて電場によって力を受ける方向にのみ等加速度直線運動で移動し、衝突により減速されると仮定する。質量$m$の自由電子が陽イオンなどと衝突してから電場中で加速され、次の陽イオンなどと衝突するまでの時間を$\tau$とする。また、自由電子は衝突した直後に、速度は0になるものと仮定する。
  • (3) 自由電子が衝突してから、その後衝突せずに時間$\tau$経過した後の自由電子の速度の大きさ(速さ)はいくらか。$I$を含んだ式で表せ。
  • (4) 自由電子の速さを時間の関数で表すグラフを書いて自由電子の平均の速さを求める方法を説明し、自由電子の平均の速さを、$I$を含んだ式で表せ。ただし、時刻0の直前で、自由電子は衝突したものとする。
• III.IIにおける自由電子の運動をじゅうぶん長い時間で平均して考えると、*2自由電子の平均の速さに比例した平均の抵抗力を自由電子が受けて、電場から受ける力とつり合い、等速直線運動をしていると近似することもできる。以降、抵抗力における比例係数(抵抗力の大きさを平均の速さで割った値)を$k$としよう。また、*3電流は金属線の断面を単位時間に通過する電気量で表されることを用いて、金属線を流れる電流について考えよう。これ以降の問題では、$k$を用いて解答し、解答に$\tau$を用いてはならない。
  • (5) 下線部*2の考え方で、自由電子の平均の速さを、$I$を含んだ式で表せ。
  • (6) 下線部*3の考え方で、電流$I$を求めよ。
  • (7) 金属線の抵抗値を、$I$を含まない式で表せ。
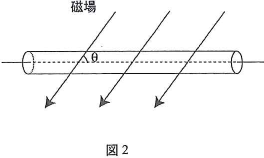
• IV.次に、金属線に電流を流したまま、図2のように、金属線の中心軸と角度$\theta$をなす方向に、磁束密度$B$の磁場を金属線全体に加えた。
  • (8) 磁場が金属線の単位長さあたりに及ぼす力の大きさを、$I$を含まない式で表せ。
• V.最後に、(8)で求めた力が鉛直上向きになるようにし、可変抵抗器の抵抗値を$R_2$にしたところ、磁場が金属線に及ぼす力と重力とがつりあった。重力加速度の大きさを$g$とし、磁場による金属線の抵抗の変化及び電流によって生じる磁場の影響は無視できるものとする。また、金属線以外の部分は、金属線に力を及ぼさないとする。
  • (9) $R_2$の値を、$I$を含まない式で表せ。