順天堂大学物理2012年第1問

次の問い(問1～問5)に答えよ。〔解答番号$\fbox{1}$～$\fbox{9}$〕

問 1 天井に固定された滑車の下にある動滑車に人の乗るゴンドラが付けられ、図1のように、滑車にかけた1本の綱の一端を人が引っ張って静止している。人の質量を$M$、ゴンドラの質量を$m$、滑車と綱の質量および摩擦は無視でき、綱は滑車にかかっている部分を除きすべて鉛直になっているものとする。下の問い((a)、(b))に答えよ。
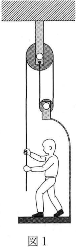
- (a) 人が綱を引いている力の大きさはいくらか。正しいものを、次の(1)～(10)のうちから一つ選べ。ただし、重力加速度の大きさを$g$とする。$\fbox{1}$
  - (1) $mg$
  - (2) $Mg$
  - (3) $\dfrac{1}{2}mg$
  - (4) $\dfrac{1}{2}Mg$
  - (5) $\dfrac{1}{3}mg$
  - (6) $\dfrac{1}{3}Mg$
  - (7) $(M+m)g$
  - (8) $\dfrac{1}{2}(M+m)g$
  - (9) $\dfrac{1}{3}(M+m)g$
  - (10) $\bigg(\dfrac{1}{3}M+\dfrac{1}{2}m\bigg)g$
- (b) このとき、ゴンドラの床から人が離れないためには、$M$と$m$の間には、 \[ \fbox{2}\geqq0 \] の関係が成り立たなければならない。$\fbox{2}$に入れるのに正しい式を、次の(1)～(8)のうちから一つ選べ。
  - (1) $M-m$
  - (2) $m-M$
  - (3) $M-2m$
  - (4) $2M-m$
  - (5) $2M-3m$
  - (6) $M-3m$
  - (7) $3M-2m$
  - (8) $3M-m$
問 2 なめらかな水平面上で、$x$軸上を速さ4 m/sで正の向きに進む質量2 kgの物体Aと、$y$軸上を速さ10 m/sで正の向きに進む質量1 kgの物体Bとが座標軸の原点で衝突し、衝突後のAは速さ2 m/sで$y$軸上を正の向きに進んだ。Bの衝突後の速度の$x$成分と$y$成分は、それぞれいくらか。正しいものを、下の(1)～(10)のうちから一つずつ選べ。
- Bの衝突後の速度の$x$成分は$\fbox{3}$ m/s
- Bの衝突後の速度の$y$成分は$\fbox{4}$ m/s
- (1) 1
- (2) 2
- (3) 3
- (4) 4
- (5) 5
- (6) 6
- (7) 7
- (8) 8
- (9) 9
- (10) 10
問 3 シャボン玉の美しい虹色は、光の反射・屈折・千渉の性質による。図2のように、シャボン膜の表面で反射する光と裏面で反射する光の道筋に経路差が生じる。その経路差によって、干渉して強めあう光の波長が異なり、見える色が変わる。シャボン膜の屈折率を$n$として、下の問い((a)、(b))に答えよ。
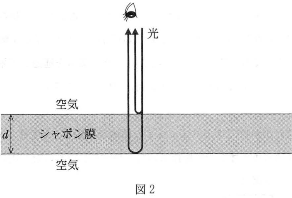
- (a) 光の速さは物質中で遅くなり、屈折率$n$の物質中では真空中の光速の$\dfrac{1}{n}$倍となる。では、真空中で波長$\lambda$の光は、屈折率$n$のシャボン膜の中で波長はいくらになるか。正しいものを、次の(1)～(9)のうちから一つ選べ。$\fbox{5}$
  - (1) $\lambda$
  - (2) $\dfrac{\lambda}{2}$
  - (3) $2\lambda$
  - (4) $n\lambda$
  - (5) $2n\lambda$
  - (6) $\dfrac{\lambda}{n}$
  - (7) $\dfrac{\lambda}{2n}$
  - (8) $\dfrac{n\lambda}{2}$
  - (9) $\dfrac{2\lambda}{n}$
- (b) 前問(a)の光が図2のように厚さ$d$のシャボン膜で干渉して強めあう条件として、正しいものを、次の(1)～(9)のうちから一つ選べ。ただし、$m$は整数である。$\fbox{6}$
  - (1) $2d=m\lambda$
  - (2) $2nd=m\lambda$
  - (3) $\dfrac{2d}{n}=m\lambda$
  - (4) $2d=\bigg(m+\dfrac{1}{2}\bigg)\lambda$
  - (5) $2nd=\bigg(m+\dfrac{1}{2}\bigg)\lambda$
  - (6) $\dfrac{2d}{n}=\bigg(m+\dfrac{1}{2}\bigg)\lambda$
  - (7) $2d=\bigg(m+\dfrac{n}{2}\bigg)\lambda$
  - (8) $2nd=\bigg(m+\dfrac{n}{2}\bigg)\lambda$
  - (9) $\dfrac{2d}{n}=\bigg(m+\dfrac{n}{2}\bigg)\lambda$
問 4 真空中で$xyz$座標の$0\leqq x\leqq d$の範囲内に、強さ$E$の一様な電界を$y$軸の正の向きにかける。いま、質量$m$、電荷$q$の正イオンが、$x$軸上を負の方向から速さ$v$で飛んできて、電界がかけてある領域を通過して飛んでいく。重力は考えなくてよいとして、次の問い((a)、(b))に答えよ。
- (a) 電界がかけてある$0\leqq x\leqq d$の領域を通過後、$x$座標が$x=2d$になった瞬間の正イオンの$y$座標はいくらか。正しいものを. 次の(1)～(10)のうちから一つ選べ。
  $y=\fbox{7}$
  - (1) $\dfrac{qEd^2}{2mv^2}$
  - (2) $\dfrac{qEd^2}{mv^2}$
  - (3) $\dfrac{3qEd^2}{2mv^2}$
  - (4) $\dfrac{2qEd^2}{mv^2}$
  - (5) $\dfrac{5qEd^2}{2mv^2}$
  - (6) $d+\dfrac{qEd^2}{2mv^2}$
  - (7) $d+\dfrac{qEd^2}{mv^2}$
  - (8) $d+\dfrac{3qEd^2}{2mv^2}$
  - (9) $d+\dfrac{2qEd^2}{mv^2}$
  - (10) $d+\dfrac{5qEd^2}{2mv^2}$
- (b) 電界がかけてある$0\leqq x\leqq d$の範囲内に、さらに磁束密度$B$の一様な磁界を$z$軸の正の向きにかけた。$x$軸上を負の方向から速さ$v$で飛んできた正イオンが、$x$軸上を直進して正の方向に飛び去るとき、$v$はいくらか。正しいものを、次の(1)～(10)のうちから一つ選べ。
  $v=\fbox{8}$
  - (1) $\dfrac{E}{B}$
  - (2) $\dfrac{2E}{B}$
  - (3) $\dfrac{qBd}{m}$
  - (4) $\dfrac{2qBd}{m}$
  - (5) $\sqrt{\dfrac{E}{B}}$
  - (6) $\sqrt{\dfrac{2E}{B}}$
  - (7) $\sqrt{\dfrac{qEd}{m}}$
  - (8) $\sqrt{\dfrac{2qEd}{m}}$
  - (9) $\dfrac{\sqrt{q^2E^2d^2+2mqEd}}{m}$
  - (10) $\dfrac{\sqrt{q^2E^2d^2-mqEd}}{m}$
問 5 外部と熱の出入りがない容器の中に液体が入っている。容器と液体は熱平衡にあり温度は$T_0$であった。容器の中の液体に熱量$Q$を加えたところ容器と液体の温度は$T_1$になった。さらにこの中に温度$T$、質量$M$の金属を入れたところ、容器と液体と中に入れた金属全体の温度は$T_2$になった。このとき、中に入れた金属の比熱を表す式は$\fbox{9}\times\dfrac{Q}{M}$となる。$\fbox{9}$に入れる式として正しいものを、次の(1)～(6)のうちから一つ選べ。
- (1) $\dfrac{T_1-T_0}{(T-T_2)(T_2-T_1)}$
- (2) $\dfrac{T_2-T_1}{(T_1-T_0)(T-T_2)}$
- (3) $\dfrac{T-T_2}{(T_2-T_1)(T_1-T_0)}$
- (4) $\dfrac{T_1-T_0}{(T-T_1)(T_2-T_1)}$
- (5) $\dfrac{T_2-T_1}{(T_1-T_0)(T-T_1)}$
- (6) $\dfrac{T-T_2}{(T-T_1)(T_1-T_0)}$