図1のように空気中に、絶縁被覆した導線を一様に巻いた断面積$S$、長さ$l$、単位長さあたりの巻数$n_1$のソレノイドコイル1があり、その上から単位長さあたりの巻数$n_2$のソレノイドコイル2を、コイル1と同じ長さ$l$になるように巻き付けた。ただし、$n_1\gt n_2$とし、コイル1の両端の端子を$a_1$、$b_1$、コイル2の両端の端子を$a_2$、$b_2$とする。コイル1の自己インダクタンスを$L_1$、コイル2の自己インダクタンスを$L_2$、コイル1とコイル2の相互インダクタンスを$M$で表す。空気の透磁率を$\mu$とし、コイル1およびコイル2の内部にできる磁界は一様であるとして、下の問い(問1～問5)に答えよ。〔解答番号$\fbox{1}$～$\fbox{7}$〕

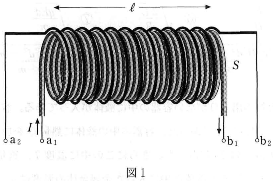
• 問 1 コイル1に電流$I$を流すとき(図1)、コイル1の内部の磁束密度はどのように表されるか。正しいものを、次の(1)～(8)のうちから一つ選べ。$\fbox{1}$
  • (1) $\mu n_1I$
  • (2) $\mu n_1lI$
  • (3) $\mu\dfrac{n_1}{S}I$
  • (4) $\mu\dfrac{n_1}{l}I$
  • (5) $n_1I$
  • (6) $n_1lI$
  • (7) $\dfrac{n_1}{S}I$
  • (8) $\dfrac{n_1}{l}I$
• 問 2 コイル1に図1の矢印の向きに流す電流$I$を時間、$\Delta t$の間に、$\Delta I$だけ増加させるとき、コイル2の端子b₂に対する端子a₂の電位は、コイル1とコイル2の相互インダクタンス$M$を用いてどのように表されるか。正しいものを、次の(1)～(8)のうちから一つ選べ。$\fbox{2}$
  • (1) $MI\Delta I$
  • (2) $-MI\Delta I$
  • (3) $\dfrac{M}{2}\Delta I\Delta t$
  • (4) $-\dfrac{M}{2}\Delta I\Delta t$
  • (5) $M\dfrac{\Delta I}{\Delta t}$
  • (6) $-M\dfrac{\Delta I}{\Delta t}$
  • (7) $\dfrac{M}{2}\bigg(\dfrac{\Delta I}{\Delta t}\bigg)^2$
  • (8) $-\dfrac{M}{2}\bigg(\dfrac{\Delta I}{\Delta t}\bigg)^2$
• 問 3 コイル1を流れる電流が変化すると問1の磁束密度が変化して、コイル2に誘導起電力が生じる。この誘導起電力を問2の結果と比較してコイル1とコイル2の相互インダクタンス$M$を求めると、$M$はいくらか。また、同様にしてコイル1の自己インダクタンス$L_1$を求めると、$L_1$はいくらか。正しいものを、下の(1)～(8)のうちから一つずつ選べ。
  • $M=\fbox{3}$
  • $L_1=\fbox{4}$
  • (1) $\mu n_1S$
  • (2) $\mu{n_1}^2S$
  • (3) $\mu{n_1}^2lS$
  • (4) $\mu \dfrac{{n_1}^2}{l}S$
  • (5) $\mu n_2S$
  • (6) $\mu n_1n_2S$
  • (7) $\mu n_1n_2lS$
  • (8) $\mu \dfrac{n_1n_2}{l}S$
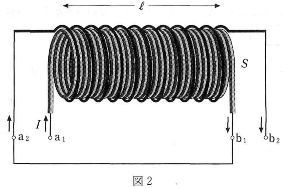
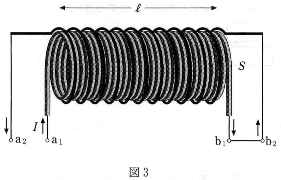
• 問 4 コイル2の両端の端子a₂、b₂が図1のようにどこにもつながっていない場合には、問2のように電流を増加させるときに外部からする仕事が、コイル1のエネルギーとして蓄えられる。いま、図2のように、コイル1の端子b₁をコイル2の端子a₂と導線でつないでからコイル1、2に電流$I$を流すと、二つのコイルに蓄えられるエネルギーの合計はいくらか。また、図3のように、コイル1の端子b₁をコイル2の端子b₂と導線でつないでからコイル1、2に電流$I$を流すと、二つのコイルに蓄えられるエネルギーの合計はいくらか。正しいものを、下の(1)～(9)のうちから一つずつ選べ。
  • 図2の二つのコイルに蓄えられるエネルギーの合計は$\fbox{5}$
  • 図3の二つのコイルに蓄えられるエネルギーの合計は$\fbox{6}$
  
  
  • (1) $\dfrac{1}{2}MI^2$
  • (2) $\dfrac{1}{2}(L_1-L_2)I^2$
  • (3) $\dfrac{1}{2}(L_1+L_2)I^2$
  • (4) $\dfrac{1}{2}(L_1-L_2+M)I^2$
  • (5) $\dfrac{1}{2}(L_1+L_2-M)I^2$
  • (6) $\dfrac{1}{2}(L_1+L_2+M)I^2$
  • (7) $\dfrac{1}{2}(L_1-L_2+2M)I^2$
  • (8) $\dfrac{1}{2}(L_1+L_2-2M)I^2$
  • (9) $\dfrac{1}{2}(L_1+L_2+2M)I^2$
• 問 5 図3の場合のコイル1の内部の磁束密度の大きさは、問1の磁束密度の大きさの何倍か。正しいものを、次の(1)～(9)のうちから一つ選べ。 $\fbox{7}$倍
  • (1) $\dfrac{n_2}{n_1}$
  • (2) $\dfrac{n_1-n_2}{n_1}$
  • (3) $\dfrac{n_1+n_2}{n_1}$
  • (4) $n_2l$
  • (5) $\dfrac{{n_2}^2}{n_1}l$
  • (6) $\dfrac{{n_1}^2-{n_2}^2}{n_1}l$
  • (7) $\dfrac{{n_1}^2+{n_2}^2}{n_1}l$
  • (8) $\dfrac{(n_1-n_2)^2}{n_1}l$
  • (9) $\dfrac{(n_1+n_2)^2}{n_1}l$