真空中において、図のように、なめらかで水平な$xy$平面上で電荷の実験を行うものとする。次の$\fbox{20}$～$\fbox{32}$に入る最も適切な式を選びなさい。ただし、電場の向き$\big(\fbox{21}$、$\fbox{23}$、$\fbox{28}$、$\fbox{30}\big)$については右図の1～8の中から正しい向きを選びなさい。1が$y$軸の正の向きで、以下時計回りに$45^\circ$ごとに番号がつけてある。クーロンの法則の比例定数を$k$とし、電位の基準点を無限遠とする。また、$a\gt0$、$Q\gt0$、$q\gt0$とする。

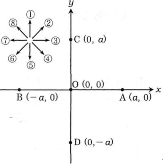
1. $x$軸上の点$\text{A}(a,0)$に電気量$Q$の点電荷を、点$\text{B}(-a,0)$に電気量$-Q$の点電荷を固定する。このとき、$y$軸上の点$\text{C}(0,a)$における電場の大きさは$kQ\times\fbox{20}$で、その向きは$\fbox{21}$である。
   $x$軸上の$x\gt{a}$の領域では電場の大きさは$kQ\times\fbox{22}$で、その向きは$\fbox{23}$である。また、同じく$x$軸上の$x\gt{a}$の領域での電位は$kQ\times\fbox{24}$である。
   ここで、$x$軸上の正方向の無限遠点に置かれた質量$m$、電気量$q$の点電荷$P$を$x$軸に沿って点$(2a,0)$まで動かす。このとき、外力がする仕事は$kQq\times\fbox{25}$である。次いで、点電荷$P$を静かに放すと、$P$は$x$軸上を正の方向に動き出す。そして、無限遠での$P$の速さは$\sqrt{kQq\times\fbox{26}}$となる。
   次に、点$\text{A}$と点$\text{B}$の点電荷はそのままにして点電荷$P$だけを取り除き、点$\text{C}$に電気量$-2\sqrt{2}Q$の点電荷を固定すると、$y$軸上の点$\text{D}(0,-a)$における電場の大きさは$kQ\times\fbox{27}$で、その向きは$\fbox{28}$である。
2. 今度は、点$\text{A}$と点$\text{B}$の両方に電気量$Q$の点電荷を固定する。このとき、点$\text{C}$における電場の大きさは$kQ\times\fbox{29}$で、その向きは$\fbox{30}$である。また、点$\text{C}$における電位は$kQ\times\fbox{31}$である。
   ここで、質量$m$、電気量$-q$の点電荷$R$を点$\text{C}$に置き、静かに放すと、$R$は原点に向かって$y$軸上を動き始め、原点での速さは$\sqrt{kQq\times\fbox{32}}$となる。
   $\fbox{20}$、$\fbox{27}$、$\fbox{29}$、$\fbox{31}$の解答群
   • (1) $\dfrac{1}{a^2}$
   • (2) $\dfrac{2}{a^2}$
   • (3) $\dfrac{\sqrt{2}}{a^2}$
   • (4) $\dfrac{\sqrt{2}}{2a^2}$
   • (5) $\dfrac{1}{2a^2}$
   • (6) $\dfrac{1}{a}$
   • (7) $\dfrac{2}{a}$
   • (8) $\dfrac{\sqrt{2}}{a}$
   • (9) $\dfrac{\sqrt{2}}{2a}$
   • (10) $\dfrac{1}{2a}$
   $\fbox{22}$、$\fbox{24}$の解答群
   • (1) $\dfrac{x^2}{x^2-a^2}$
   • (2) $\dfrac{a^2}{x^2-a^2}$
   • (3) $\dfrac{2x}{x^2-a^2}$
   • (4) $\dfrac{2a}{x^2-a^2}$
   • (5) $\dfrac{1}{x^2-a^2}$
   • (6) $\dfrac{2(x^2+a^2)}{(x-a)^2(x+a)^2}$
   • (7) $\dfrac{x^2}{(x-a)^2(x+a)^2}$
   • (8) $\dfrac{a^2}{(x-a)^2(x+a)^2}$
   • (9) $\dfrac{4ax}{(x-a)^2(x+a)^2}$
   • (10) $\dfrac{1}{(x-a)^2(x+a)^2}$
   $\fbox{25}$の解答群
   • (1) $\dfrac{1}{4a}$
   • (2) $\dfrac{1}{3a}$
   • (3) $\dfrac{1}{2a}$
   • (4) $\dfrac{2}{3a}$
   • (5) $\dfrac{3}{4a}$
   • (6) $\dfrac{1}{a}$
   • (7) $\dfrac{4}{3a}$
   • (8) $\dfrac{3}{2a}$
   • (9) $\dfrac{2}{a}$
   • (10) $\dfrac{3}{a}$
   $\fbox{26}$の解答群
   • (1) $\dfrac{3ma}{2}$
   • (2) $\dfrac{3ma}{4}$
   • (3) $\dfrac{2m}{3a}$
   • (4) $\dfrac{4m}{3a}$
   • (5) $\dfrac{3a}{2m}$
   • (6) $\dfrac{3a}{4m}$
   • (7) $\dfrac{2a}{3m}$
   • (8) $\dfrac{4a}{3m}$
   • (9) $\dfrac{2}{3ma}$
   • (10) $\dfrac{4}{3ma}$
   $\fbox{32}$の解答群
   • (1) $\dfrac{4-2\sqrt{2}}{ma}$
   • (2) $\dfrac{ma}{4-2\sqrt{2}}$
   • (3) $\dfrac{(4-2\sqrt{2})m}{a}$
   • (4) $\dfrac{a}{(4-2\sqrt{2})m}$
   • (5) $\dfrac{(4-2\sqrt{2})a}{m}$
   • (6) $\dfrac{2\sqrt{2}}{ma}$
   • (7) $\dfrac{ma}{2\sqrt{2}}$
   • (8) $\dfrac{2\sqrt{2}m}{a}$
   • (9) $\dfrac{a}{2\sqrt{2}m}$
   • (10) $\dfrac{2\sqrt{2}a}{m}$