自然の長さが$L$で、ばね定数が$k$の軽いばねがある。図1のように、このばねの一端に質量$m$の小物体$\text{A}$を取りつけて、水平面と角度$\theta$をなす滑らかな斜面上に置き、ばねの他端は斜面の最下端$\text{C}$に固定する。次に質量$m$の小物体$\text{B}$を軽くて伸びない糸で$\text{A}$と結び、滑らかな滑車を通して鉛直につるす。重力加速度の大きさを$g$とする。なお、以下の問題文中で「ばねの伸び」とあるのはすべて「自然の長さからのばねの伸び」の意味である。

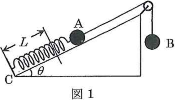
• (1) $\text{A}$、$\text{B}$をつりあいの状態におくとき、ばねの伸び$d_1$は$\fbox{1}\times \left(\fbox{2}\right)$と表される。このとき、ばねの弾性エネルギーは$\fbox{3}\times (d_1)^2$である。
• (2) 設問(1)の状態から、$\text{B}$を鉛直真下に引き下げて、ある位置に止めてから静かに手を放すと、$\text{A}$と$\text{B}$は運動を始めた。このとき糸のたるみはないものとすると、ばねの伸びが$d_2$のとき、系の張力の大きさは、$\fbox{4}\times\left(\fbox{5}\right)+\fbox{6}\times d_2$である。
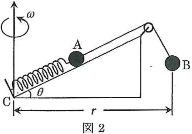
• (3) 設問(1)の状態から、$\text{A}$、$\text{B}$を斜面とともに一定の角速度$\omega$で、$\text{C}$を通る鉛直軸のまわりに回転させたところ、図2の状態でつり合った($\text{A}$と$\text{B}$は回転軸を含む同一鉛直面内にある)。回転軸から$\text{B}$までの距離を$r$とすると、ばねの伸びは、 $$\dfrac{m\times\left(\fbox{7}+\sqrt{g^2+\fbox{8}}\right)}{k-\fbox{9}}$$ である。
  

• $\fbox{1}$、$\fbox{3}$、$\fbox{4}$、$\fbox{6}$の解答群
  • (1) $\dfrac{g}{2}$
  • (2) $\dfrac{k}{2}$
  • (3) $\dfrac{mg}{2}$
  • (4) $\dfrac{m}{k}$
  • (5) $\dfrac{2m}{k}$
  • (6) $\dfrac{mg}{k}$
  • (7) $\dfrac{k}{m}$
  • (8) $\dfrac{k}{2m}$
  • (9) $\dfrac{k}{mg}$
  • (10) $\dfrac{k}{2mg}$
• $\fbox{2}$、$\fbox{5}$の解答群
  • (1) $1+\sin\theta$
  • (2) $2+\sin\theta$
  • (3) $1+\cos\theta$
  • (4) $2+\cos\theta$
  • (5) $1-\sin\theta$
  • (6) $2-\sin\theta$
  • (7) $1-\cos\theta$
  • (8) $2-\cos\theta$
• $\fbox{7}$の解答群
  • (1) $L\omega^2\sin^2\theta+g\sin\theta$
  • (2) $L\omega^4\sin^2\theta+g\sin\theta$
  • (3) $L\omega^2\cos^2\theta+g\sin\theta$
  • (4) $L\omega^4\cos^2\theta+g\sin\theta$
  • (5) $L\omega^2\sin^2\theta-g\sin\theta$
  • (6) $L\omega^4\sin^2\theta-g\sin\theta$
  • (7) $L\omega^2\cos^2\theta-g\sin\theta$
  • (8) $L\omega^4\cos^2\theta-g\sin\theta$
• $\fbox{8}$の解答群
  • (1) $r\omega$
  • (2) $r\omega^2$
  • (3) $r\omega^4$
  • (4) $r^2\omega$
  • (5) $r^2\omega^2$
  • (6) $r^2\omega^4$
  • (7) $r^4\omega$
  • (8) $r^4\omega^2$
  • (8) $r^4\omega^4$
• $\fbox{9}$の解答群
  • (1) $\omega^2\sin^2\theta$
  • (2) $\omega^2\cos^2\theta$
  • (3) $\omega^4\sin^2\theta$
  • (4) $\omega^4\cos^2\theta$
  • (5) $m\omega^2\sin^2\theta$
  • (6) $m\omega^2\cos^2\theta$
  • (7) $m\omega^4\sin^2\theta$
  • (8) $m\omega^4\cos^2\theta$