水平面上の点$\text{O}$を通る鉛直線上に設置した太さを無視できる細いガラス管に、伸び縮みしない細くて軽い糸を通し、その両端にそれぞれ質量$M$の小球$\text{A}$と質量$m$の小球$\text{B}$を取り付ける。次に、小球$\text{A}$を図のように水平面と平行な面内で等速円運動させたところ、小球$\text{B}$は鉛直線上で静止した状態になった。ガラス管の上端を$\text{P}$、円運動の中心を$\text{Q}$、$\text{AP}=l$、$\text{QO}=h$、円運動の半径$\text{AQ}=r$、重力加速度の大きさを$g$として、$\fbox{1}$～$\fbox{4}$に入る最も適切な数式または数値を選びなさい。ただし、糸とガラス管との間の摩擦力や空気抵抗は無視できるものとする。

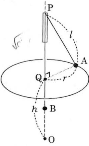
1. 小球$\text{A}$の受ける円運動の向心力の大きさは、$Mg\times\fbox{1}$である。
   $\fbox{1}$の解答群
   • (1) $\dfrac{l}{r}$
   • (2) $\dfrac{r}{l}$
   • (3) $\dfrac{\sqrt{l^2+r^2}}{l}$
   • (4) $\dfrac{\sqrt{l^2-r^2}}{l}$
   • (5) $\dfrac{\sqrt{l^2+r^2}}{r}$
   • (6) $\dfrac{\sqrt{l^2-r^2}}{r}$
   • (7) $\dfrac{l}{\sqrt{l^2+r^2}}$
   • (8) $\dfrac{l}{\sqrt{l^2-r^2}}$
   • (9) $\dfrac{r}{\sqrt{l^2+r^2}}$
   • (10) $\dfrac{r}{\sqrt{l^2-r^2}}$
2. 小球$\text{A}$が30回転する時間を測定したら24.0秒で、このとき$l=64~[\text{cm}]$であった。重力加速度の大きさを$9.8~[\text{m}/\text{s}^2]$、$\pi=3.14$とすると、小球$\text{B}$と小球$\text{A}$の質量比$\dfrac{m}{M}=\fbox{2}$となる。
   $\fbox{2}$の解答群
   • (1) 0.50
   • (2) 0.74
   • (3) 1.1
   • (4) 1.6
   • (5) 2.1
   • (6) 2.7
   • (7) 3.2
   • (8) 3.7
   • (9) 4.0
   • (10) 4.8
3. 小球$\text{A}$が速さ$v$で円運動を続けている最中に突然糸が切れて、小球$\text{A}$は$\text{O}$を含む水平面上に落下した。$v$および先に定義した$l$、$r$、$h$、$g$のうち必要なものを用いて表すと、水平面上の落下地点と$\text{O}$の間の距離は$\fbox{3}$であり、水平面に達したときの小球$\text{A}$の速さは$\fbox{4}$である。
   $\fbox{3}$の解答群
   • (1) $r+\sqrt{\dfrac{v^2h}{g}}$
   • (2) $r+\sqrt{\dfrac{2v^2h}{g}}$
   • (3) $r+\sqrt{\dfrac{(vh)^2}{g(l^2+r^2)}}$
   • (4) $r+\sqrt{\dfrac{2(vh)^2}{g(l^2+r^2)}}$
   • (5) $\sqrt{r^2+\dfrac{v^2h}{g}}$
   • (6) $\sqrt{r^2+\dfrac{2v^2h}{g}}$
   • (7) $\sqrt{r^2+\dfrac{(vh)^2}{g(l^2+r^2)}}$
   • (8) $\sqrt{r^2+\dfrac{2(vh)^2}{g(l^2+r^2)}}$
   $\fbox{4}$の解答群
   • (1) $\sqrt{gh}$
   • (2) $\sqrt{2gh}$
   • (3) $2\sqrt{gh}$
   • (4) $v+\sqrt{gh}$
   • (5) $v+\sqrt{2gh}$
   • (6) $v+2\sqrt{gh}$
   • (7) $\sqrt{v^2+gh}$
   • (8) $\sqrt{v^2+2gh}$
   • (9) $\sqrt{v^2+4gh}$