なめらかな水平面上に静止している質量$m$の小球$\text{B}$に、質量$M$の小球$\text{A}$を速さ$U$で弾性衝突させたところ、$\text{A}$は衝突前の運動方向から左へ$45^\circ$の向きに速さ$V$で進み、$\text{B}$は右へ$30^\circ$の向きに速さ$v$で進んだ。外力は一切作用せず、また小球は回転しないものとして、$\fbox{13}$～$\fbox{19}$に入る最も適切な数値を選びなさい。
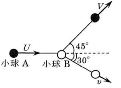運動量保存の法則より、 \[\left\{\begin{array}{l}2MU&=\fbox{13}MV+\fbox{14}mv\\0&=\fbox{15}MV-mv\end{array} \right.\] 弾性衝突なので、力学的エネルギーが保存され、次式が成り立つ。 \[\frac{1}{2}MU^2=\frac{1}{2}MV^2+\frac{1}{2}mv^2\] 以上の式より、
$\dfrac{M}{m}=\dfrac{\fbox{16}}{\fbox{17}}$であり、$\dfrac{V}{v}=\dfrac{\fbox{18}}{\fbox{19}}$である。
$\fbox{13}$～$\fbox{19}$の解答群

• (1) 1
• (2) 2
• (3) 3
• (4) $\sqrt{2}$
• (5) $\sqrt{2}$
• (6) $(1+\sqrt{2})$
• (7) $(1+2\sqrt{2})$
• (8) $(1+\sqrt{3})$
• (9) $(1+2\sqrt{3})$