関西医科大学数学2013年第4問

$\triangle{\text{ABC}}$ において、

$\overrightarrow{\text{AB}}=\vec{k}$ 、

$\overrightarrow{\text{AC}}=\vec{l}$ とする。ベクトルの大きさについて、

$|\vec{k}|=2$ 、

$|\vec{l}|=\sqrt{3}+1$ 、

$|\sqrt{3}\vec{k}-\vec{l}|=10$ が成り立っている。このとき、

$\triangle{\text{ABO}}$ の外心を

$\text{O}$ として、以下の問いに答えよ。

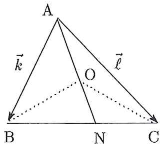
(1)内積 $\vec{k}\cdot\vec{l}$ の値を $\fbox{ヌ}$ に記入し、 $\angle{\text{BAC}}$ の大きさを $\fbox{ネ}$ に記入せよ。
(2)辺 $\text{BC}$ の長さを $\fbox{ノ}$ に記入し、 $\angle{\text{ACB}}$ の大きさを $\fbox{ハ}$ に記入せよ。
(3)直線 $\text{AO}$ と辺 $\text{BC}$ との交点を $\text{N}$ とする。ベクトル $\overrightarrow{\text{AN}}$ を $\vec{k}$ 、 $\vec{l}$ を用いて表した式を $\fbox{ヒ}$ に記せ。