円運動する荷電粒子を、軌道半径を変えないで加速する方法として、与える磁場の変化による誘導電場を用いるベータトロンと呼ばれる装置がある。この原理について考えてみよう。

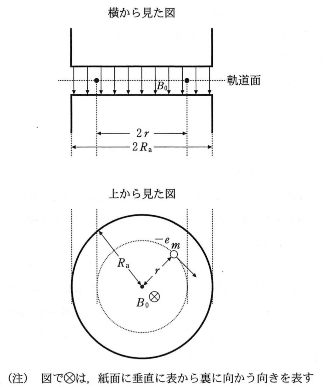
まず図のように、真空中において、半径$R_a$の円柱形の鉄心を持つ電磁石の磁極のすき間に、磁束密度$B_0$の一様な磁場を下向きに与えた場合を考える。重力の影響は無視できるとする。この磁場の中を図のように電荷$-e~(e\gt0)$、質量$m$の電子が半径$r$で等速円運動しているとき、電子の速度を$v$とすれば、$v$は$m$、$r$、$e$、$B_0$を用いて$v=\fbox{1}$と表すことができる。また電子が軌道を1周回るのにかかる時間は$m$、$e$、$B_0$を用いて$\fbox{2}$なので、電子の軌道断面を単位時間当たりに通過する電気量、すなわち電流は$m$、$e$、$B_0$を用いて$\fbox{3}$と書ける。これは半径$r$の抵抗のない円環に電流が流れているものと見なすことができる。

この円環に磁場変化を与えてみよう。磁極間の磁束密度を一様に保ちながら、時間$\Delta t$の間に$\Delta B$だけ均一に増加させると、円環に誘起される起電力は円環を貫く磁束の単位時間あたりの変化で与えられ、その大きさは$\fbox{4}$である。そのとき円環上の電場の大きさは$\fbox{5}$となり、これによって円環には電流が誘導される。円環に電流が誘導されるということは、電子が誘導電場$\fbox{5}$により、大きさ$\fbox{6}$の力を受けて加速されることと等価である。このとき、電子が受けた力積は電子の運動量の変化に等しいので、時間$\Delta t$後の速さが$\Delta v=\fbox{7}$だけ増えたことになり、電子に働く中心方向の合力は$v$、$\Delta v$、$B_0$、$\Delta B$、$m$、$e$、$r$を用いて表すと$\fbox{8}$となる。$\Delta v$、$\Delta B$は微小量として$(\Delta v)^2$、$(\Delta B)(\Delta v)$を無視する近似を行えば、中心方向の合力$\fbox{8}$は$\Delta B$に比例して$\fbox{9}$と書き表すことができる。このように磁極間に一様で、均一な磁場変化を与えて電子を加速した場合には、軌道半径が$\fbox{A}$ことがわかる。実際のベータトロンでは、この影響を消して、電子が軌道半径を変えないで加速されるために、磁極間の磁場分布は一様ではなく、与える磁場変化も均一にならない工夫がなされている。

• (1) 上の文中の$\fbox{1}$から$\fbox{9}$までに入る適当な数式または言葉を解答欄の該当箇所に記入せよ。
• (2) 上の文中の$\fbox{A}$に入る適当な文を下記の選択肢の中から選び、解答欄に文の前に付けられた記号を記入せよ。
  選択肢：
  • ア：大きくなる
  • イ：変わらない
  • ウ：小さくなる