川崎医科大学物理2013年第1問
次の問いに対して、最も適切なものを選択肢の中から一つ選びなさい。
- (1) 図1のように$xy$平面内にばねがつながった金属棒、内部抵抗の無視できる起電力$E$の電池、抵抗値$R$の抵抗、スイッチで成り立っている回路がある。ばねのばね定数は$k$で、金属棒の中心につながっているとする。導線$\text{ab}$と導線$\text{cd}$は$x$軸に平行で距離$l$だけ離れて設置されている。また、金属棒はその導線の上に$y$軸に平行に置かれている。磁束密度$B$の磁界が紙面に垂直に表から裏に向けてかけられているとして、次の問いに答えなさい。なお、金属棒と導線には抵抗はなく、金属棒と導線の間の摩擦も無視できるものとする。さらに、回路を流れる電流が作る磁界も無視できるものとする。
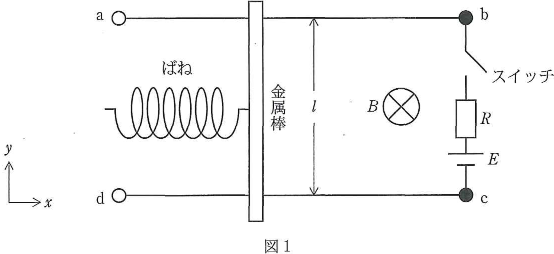
- 問1 金属棒につながれていない方のばねの端を自然長で固定する。この状態で回路のスイッチを入れると、金属棒が移動したのち静止した。
- (a) 静止した金属棒に流れる電流はいくらか。$\fbox{ア}$
$\fbox{ア}$の選択肢- (1) $0$
- (2) $Bl$
- (3) $\dfrac{Bl}{R}$
- (4) $\dfrac{R}{Bl}$
- (5) $BlR$
- (6) $\dfrac{E}{R}$
- (7) $ER$
- (b) 金属棒が移動した方向は、$x$軸の正方向か、それとも負方向か。また、金属棒が移動した距離はいくらか。$\fbox{イ}$
$\fbox{イ}$の選択肢- (1) $x$軸の正方向に$\dfrac{Bl}{k}$移動
- (2) $x$軸の負方向に$\dfrac{Bl}{k}$移動
- (3) $x$軸の正方向に$\dfrac{Bl}{kR}$移動
- (4) $x$軸の負方向に$\dfrac{Bl}{kR}$移動
- (5) $x$軸の正方向に$\dfrac{EBl}{kR}$移動
- (6) $x$軸の負方向に$\dfrac{EBl}{kR}$移動
- (7) $x$軸の正方向に$\dfrac{EBR}{k}$移動
- (8) $x$軸の負方向に$\dfrac{EBR}{k}$移動
- (a) 静止した金属棒に流れる電流はいくらか。$\fbox{ア}$
- 問2 問1の状態でばねの固定を外し、この端に$x$軸の負方向の外力を加えたところ、金属棒は一定の速さ$v$で$x$軸方向に運動するようになった。ただし、一定の速さで運動している間、ばねの長さは一定に保たれていた。
- (a) この運動により、回路を貫く磁束が単位時間当たり$\fbox{ウ}$だけ変化するため、回路に大きさが$\fbox{エ}$で向きが$y$軸の$\fbox{オ}$方向の誘導起電力が発生する。その結果、金属棒には、大きさ$\fbox{カ}$の電流が流れる。
$\fbox{ウ}$、$\fbox{エ}$、$\fbox{オ}$、$\fbox{カ}$の選択肢(同じものを繰り返し選択してもよい)- (1) $0$
- (2) $\dfrac{E}{R}$
- (3) $\dfrac{EBl}{R}$
- (4) $\dfrac{vBl}{R}$
- (5) $\dfrac{E+vBl}{R}$
- (6) $\dfrac{E-vBl}{R}$
- (7) $B$
- (8) $Bl$
- (9) $vB$
- (0) $vBl$
- (+) $正$
- (-) $負$
- (b)ばねの伸びはいくらか。$\fbox{キ}$
$\fbox{キ}$の選択肢- (1) $0$
- (2) $\dfrac{E}{kR}$
- (3) $\dfrac{EBl}{kR}$
- (4) $\dfrac{vBl}{kR}$
- (5) $\dfrac{vB^2l^2}{kR}$
- (6) $\dfrac{v^2B^2l^2}{kR}$
- (7) $\dfrac{Bl(E+vBl)}{kR}$
- (8) $\dfrac{Bl(E-vBl)}{kR}$
- (c) 電池の消費電力はいくらか。$\fbox{ク}$
- (d) 金属棒が等速運動をしているとき、外力の仕事率はいくらか。$\fbox{ケ}$
- (e) 抵抗から発生する単位時間あたりのジュール熱はいくらか。$\fbox{コ}$
$\fbox{ク}$、$\fbox{ケ}$、$\fbox{コ}$の選択肢(同じものを繰り返し選択してもよい)- (1) $0$
- (2) $\dfrac{E^2}{R}$
- (3) $\dfrac{EvBl}{R}$
- (4) $\dfrac{E(E+vBl)}{R}$
- (5) $\dfrac{E(E-vBl)}{R}$
- (6) $\dfrac{v^2B^2l^2}{R}$
- (7) $\dfrac{vBl(E+vBl)}{R}$
- (8) $\dfrac{vBl(E-vBl)}{R}$
- (9) $\dfrac{Bl(E+vBl)}{R}$
- (0) $\dfrac{Bl(E-vBl)}{R}$
- (+) $\dfrac{(E+vBl)^2}{R}$
- (-) $\dfrac{(E-vBl)^2}{R}$
- (a) この運動により、回路を貫く磁束が単位時間当たり$\fbox{ウ}$だけ変化するため、回路に大きさが$\fbox{エ}$で向きが$y$軸の$\fbox{オ}$方向の誘導起電力が発生する。その結果、金属棒には、大きさ$\fbox{カ}$の電流が流れる。
- 問1 金属棒につながれていない方のばねの端を自然長で固定する。この状態で回路のスイッチを入れると、金属棒が移動したのち静止した。
- (2)
- 問1 真空中で速さ$c$、波長$\lambda$の光が屈折率$n$の物質に入ったとき、物質中の波長は$\fbox{サ}$、振動数は$\fbox{シ}$となる。
- 問2 水の屈折率を$n$とする。水中の深さ$h$の点にある物体を真上付近から見ると、光が水面で$\fbox{ス}$するため、物体は深さが$\fbox{セ}$の点にあるように見える。ただし角度$\theta$が小さいとき、$\sin\theta\fallingdotseq\tan\theta$とする。物体の真上の水面上の点から、水面に沿ってだんだん離れていくと、真上の点からの距離が$\fbox{ソ}$の点で物体は見えなくなる。これは、水面で光が$\fbox{タ}$するためである。
- 問3 水中のレンズの焦点距離は、空気中と比べて$\fbox{チ}$。ただし、空気、水、レンズの材質の屈折率を、それぞれ1、1.3、1.5とする。
- 問4 凸レンズの形は変えず、材質を屈折率の大きいものに変えると、焦点距離は$\fbox{ツ}$。
$\fbox{サ}$、$\fbox{シ}$の選択肢(同じものを繰り返し選択してもよい)- (1) $n\lambda$
- (2) $\dfrac{\lambda}{n}$
- (3) $\dfrac{n}{\lambda}$
- (4) $nc$
- (5) $\dfrac{c}{n}$
- (6) $\dfrac{n}{c}$
- (7) $\dfrac{\lambda}{c}$
- (8) $\dfrac{c}{\lambda}$
- (1) 回折
- (2) 分散
- (3) 屈折
- (4) 偏光
- (5) 全反射
- (6) 透過
- (7) 散乱
- (8) 直進
- (1) $nh$
- (2) $\dfrac{h}{n}$
- (3) $\dfrac{n}{h}$
- (4) $h$
- (5) $h\sqrt{n^2-1}$
- (6) $\dfrac{h}{\sqrt{n^2-1}}$
- (7) $\dfrac{\sqrt{n^2-1}}{h}$
- (8) $\sqrt{n^2+h^2}$
- (1) 短くなる
- (2) 変化しない
- (3) 長くなる
- 問5 赤、黄、緑、青、紫の光を同じレンズに入射させたとき、焦点距離は$\fbox{テ}$。
- 問6 焦点距離$f$の凸レンズで、物体の像の倍率を$1$とするためには、レンズから物体までの距離を$\fbox{ト}$とすればよい。
$\fbox{テ}$の選択肢- (1) 赤が最も短い
- (2) 黄が最も短い
- (3) 緑が最も短い
- (4) 青が最も短い
- (5) 紫が最も短い
- (6) どの色も等しい
- (1) $f$
- (2) $\dfrac{1}{f}$
- (3) $2f$
- (4) $\dfrac{f}{2}$
- (5) $\dfrac{2}{f}$
- (6) $f^2$
- (7) $\sqrt{f}$
- 問7格子定数$d$の回折格子に、波長$\lambda$の光を垂直に入射させると、後方のスクリーンに明暗の縞模様ができた。中央の最も明るい明線の隣の明線を1次の明線、その次の明線を2次の明線とする。光の入射方向と、1次、2次の明線方向とのなす角をそれぞれ$\theta_1$、$\theta_2$とすると(図2)、$\dfrac{\sin\theta_2}{\sin\theta_1}=\fbox{ナ}$となる。
$\fbox{ナ}$の選択肢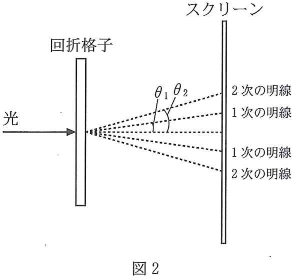
- (1) $2$
- (2) $2\lambda$
- (3) $\dfrac{2\lambda}{d}$
- (4) $\dfrac{2d}{\lambda}$
- (5) $\dfrac{1}{2}$
- (6) $\dfrac{\lambda}{2}$
- (7) $\dfrac{d}{2\lambda}$
- (8) $\dfrac{\lambda}{2d}$