川崎医科大学物理2012年第1問

次の問いに対して、最も適切なものを選択肢の中から一つ選びなさい。

I.摩擦の無視できるなめらかで水平な床がある。高さhから、この床に小球を衝突させる。床と小球とのはねかえり係数をe (0<e<1)、重力加速度をgとして、次の問いに答えなさい。
1. 図1のように、小球を初速度0で真下へ落下させた。
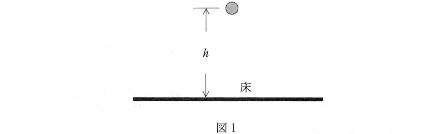
  - (a) 床に衝突する直前の小球の速さはいくらか。 $\fbox{ア}$
  - (b) 床に衝突直後の小球の速さはいくらか。イ
    ア、イの選択肢(同じものを繰り返し選択してもよい)
    - (1) $\sqrt{gh}$
    - (2) $\sqrt{mgh}$
    - (3) $\sqrt{2gh}$
    - (4) $\sqrt{2mgh}$
    - (5) $e\sqrt{gh}$
    - (6) $e\sqrt{mgh}$
    - (7) $e\sqrt{2gh}$
    - (8) $e\sqrt{2mgh}$
    - (9) $0$
  - (c) 衝突後の小球の力学的エネルギーを衝突前と比較すると, 正しい関係はどれか。ウ
    ウの選択肢
    - (1) 衝突前と同じ。
    - (2) 衝突前より減る。
    - (3) 衝突前より増える。
2. 図2のように、鉛直に対し角度θの方向に初速度v0で小球を投げおろした。この小球が、床に衝突する直前の入射角をθ′、衝突直後の反射角をθ″とする(図3) 。
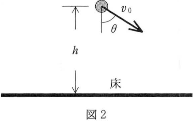
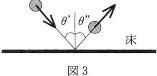
  - (a) \tan\theta'はいくらか。\fbox{エ}
    \fbox{エ}の選択肢
    - (1) $\tan\theta$
    - (2) $\dfrac{v_0\sin\theta}{\sqrt{2gh+v_o^2\cos^2\theta}}$
    - (3) $\dfrac{\sqrt{2gh+v_o^2\cos^2\theta}}{ v_0\sin\theta }$
    - (4) $\dfrac{v_0\sin\theta}{\sqrt{gh+v_o^2\cos^2\theta}}$
    - (5) $\dfrac{\sqrt{gh+v_o^2\cos^2\theta}}{ v_0\sin\theta }$
    - (6) $\dfrac{\sqrt{2gh}}{v_0sin\theta}$
  - (b) 衝突後の速さはいくらか。\fbox{オ}
    \fbox{オ}の選択肢
    - (1) $ev_0$
    - (2) $e\sqrt{v_0^2+2gh}$
    - (3) $e\sqrt{v_0^2+gh}$
    - (4) $\sqrt{v_0^2\sin^2\theta+2e^2gh+e^2v_0^2\cos^2\theta}$
    - (5) $\sqrt{v_0^2\sin^2\theta+e^2gh+e^2v_0^2\cos^2\theta}$
  - (c) \tan\theta’’はいくらか。\fbox{カ}
    - (1) $\tan\theta$
    - (2) $\dfrac{v_0\sin\theta}{e\sqrt{2gh+v_o^2\cos^2\theta}}$
    - (3) $\dfrac{e\sqrt{2gh+v_o^2\cos^2\theta}}{ v_0\sin\theta }$
    - (4) $\dfrac{v_0\sin\theta}{e\sqrt{gh+v_o^2\cos^2\theta}}$
    - (5) $\dfrac{e\sqrt{gh+v_o^2\cos^2\theta}}{ v_0\sin\theta }$
    - (6) $\dfrac{e\sqrt{2gh}}{v_0sin\theta}$
  - (d) 衝突後の小球が到達する最高点の高さはいくらか。 \fbox{キ}
    \fbox{キ}の選択肢
    - (1) $h$
    - (2) $e^2h$
    - (3) $\dfrac{e^2h}{2}$
    - (4) $\dfrac{e^2(gh+v_0^2\cos^2\theta) }{2g}$
    - (5) $\dfrac{e^2(gh+v_0^2\cos^2\theta) }{2g}$
    - (6) $\dfrac{e^2(gh+v_0^2) }{2g}$
    - (7) $\dfrac{e^2(2gh+v_0^2) }{2g}$
II.電気抵抗、電池および電流計からなる図4のような回路がある。ただし、電池および電流計の内部抵抗は無視できるものとする。
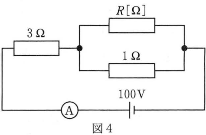
1. 回路の合成抵抗は\fbox{ク}[\Omega]である。
  \fbox{ク}の選択肢
  - (1) $4+R$
  - (2) $\dfrac{1+4R}{R}$
  - (3) $\dfrac{3+4R}{3R}$
  - (4) $\dfrac{3+4R}{1+R}$
  - (5) $\dfrac{R}{1+4R}$
  - (6) $\dfrac{3R}{3+4R}$
  - (7) $\dfrac{1+R}{3+4R}$
2. 電流計の値を30[\text{A}]とするには、Rの値は\fbox{ケ}[\Omega]でなければならない。
  \fbox{ケ}の選択肢
  - (1) 0.3
  - (2) 0.5
  - (3) 0.7
  - (4) 1
  - (5) 1.5
  - (6) 3
  - (7) 5
  - (8) 7
  - (9) 10
  - (10) 15
3. 問2で求めたRの抵抗値を直径2[\text{mm}]の二クロム線で作ることにすると、ニクロム線の長さは\fbox{コ}[\text{m}]となる。ただし、ニクロム線の抵抗率は1.0×10^{-6}[\Omega\cdot m]とし、この値は温度によって変化しないものとする。 \fbox{コ}の選択肢
  - (1) 0.9
  - (2) 1.6
  - (3) 2.2
  - (4) 3.1
  - (5) 3.8
  - (6) 4.7
  - (7) 6.3
  - (8) 8.8
  - (9) 13
  - (10) 19
4. 電池から電流30[\text{A}]を1分間流したとすると、3で作った二クロム線の抵抗で発生するジュール熱は\fbox{サ}[\text{J}]となる。
  \fbox{サ}の選択肢
  - (1) $1.0\times10^2$
  - (2) $1.4\times10^2$
  - (3) $2.0\times10^2$
  - (4) $3.3\times10^2$
  - (5) $4.0\times10^3$
  - (6) $6.0\times10^3$
  - (7) $9.0\times10^3$
  - (8) $1.2\times10^4$
  - (9) $2.0\times10^4$
III.
1. 質量m[\text{kg}]、運動量p[\text{kg}~\text{m}/\text{s}]の粒子のド・ブロイ波長は、\lambda=\fbox{シ}[\text{m}]である。ここでhは\fbox{ス}定数で、その単位は\fbox{セ}である。\fbox{ス}定数は10^{-33}程度の値なので、質量10^{-30~}[\text{kg}]、速さ10^6[\text{m}/\text{s}]の粒子のド・ブロイ波長は、およそ\fbox{ソ}[\text{nm}]である。
  \fbox{シ}の選択肢
  - (1) $\dfrac{1}{2}hp$
  - (2) $hp$
  - (3) $\dfrac{h}{2p}$
  - (4) $\dfrac{h}{p}$
  - (5) $\dfrac{hp^2}{2m}$
  - (6) $\dfrac{hp}{m}$
  \fbox{ス}の選択肢
  - (1) アインシュタイン
  - (2) ニュートン
  - (3) ミリカン
  - (4) リュードベリ
  - (5) プランク
  - (6) ポーア
  - (7) ド・ブロイ
  - (8) ラザフォード
  \fbox{セ}の選択肢
  - (1) $\text{s}/\text{kg}$
  - (2) $\text{Js}$
  - (3) $\text{m}/\text{J}$
  - (4) $\text{s}$
  - (5) $\text{kg}\ \text{m}/\text{s}$
  - (6) $\text{J}$
  \fbox{ソ}の選択肢
  - (1) 0.001
  - (2) 0.01
  - (3) 0.1
  - (4) 1
  - (5) 10
  - (6) 100
  - (7) 1000
2. 半導体における電流のにない手を\fbox{タ}といい、n型半導体の\fbox{タ}は\fbox{チ}で、p型半導体の\fbox{タ}は\fbox{ツ}である。また、半導体を利用すると、例えば発光ダイオードでは、\fbox{テ}変えることができ、太陽電池では\fbox{ト}変えることができる。
  \fbox{タ}、\fbox{チ}、\fbox{ツ}の選択肢（同じものを繰り返し選択してもよい）
  - (1) アクセプタ
  - (2) キャリア
  - (3) ドナー
  - (4) エミッタ
  - (5) コレクタ
  - (6) 電子
  - (7) ホール
  - (8) $\alpha$ 粒子
  \fbox{テ}、\fbox{ト}の選択肢（同じものを繰り返し選択してもよい）
  - (1) 電気エネルギーを音に
  - (2) 電気エネルギーを磁気に
  - (3) 電気エネルギーを光に
  - (4) 音エネルギーを電気に
  - (5) 磁気エネルギーを電気に
  - (6) 光エネルギーを電気に