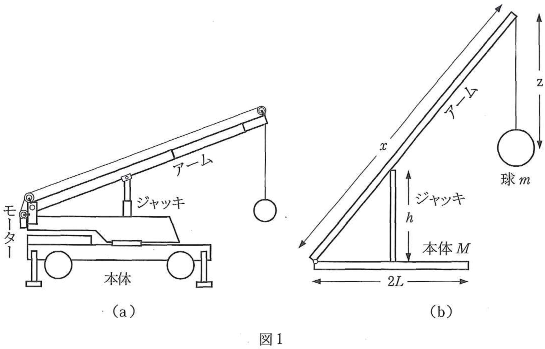
クレーン車（図1(a)）の安定性について、図1(b)のように模式化して考える。質量$M$のクレーン車本体を、水平に置いた1辺の長さ$2L$の一様な正方形の板で表す。1辺の中央に長さ$x$の棒(アーム)をちょうつがいで固定し、本体中央で垂直に伸縮する1本の棒(ジャッキ)で支える。アーム、本体、ジャッキの厚みは無視でき、アームとジャッキの質量も無視できる。

クレーンに質量$m$、半径$a$の球をつるした。ジャッキの高さを$h$、アームの先端から球の中心までの距離を$z$とし、重力加速度を$g$とする。

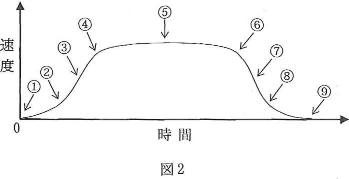
• 問1 モーターを起動して、図2に示す速度で球を上方に引き上げるとき、アームの先端が下向きに受ける力が最大になるのはどこか。図中の番号で答えよ。
• 問2 この球を一定速度$v$で引き上げるときのモーターの消費電力を求めよ。モーターの仕事効率を100%とする。
• 問3 アームの長さを$x$に保ったままジャッキをある高さ$h$までゆっくり下げたとき、クレーンは倒れ始めた。このときの$h$を、$M$、$m$、$L$、$x$、$z$、$g$から必要な記号を使って表せ。ただし、球をつるしたロープは鉛直下向きを維持するものとする。

アームから球の向きに水平な風が吹き始めた(図3)。

風速$v$[m/s]の空気の流れの中で、半径$a$[m]の球が受ける力は$F_1=k_1a^2v^2$と表される。いっぽう、長さ$x$[m]、幅$b$[m]のアームは、水平な力$F_2=k_2bxv^2\sin\theta$を全体で一様に受ける。アームと本体とのなす角を$\theta$とし、$k_1=1.0$kg・m^-3、$k_2=1.5$kg・m^-3とする。

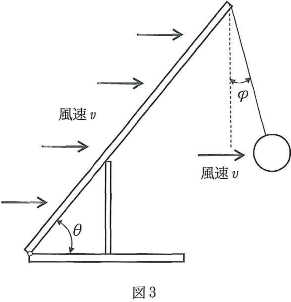
• 問4 風がゆっくりと強くなってロープが鉛直方向となす角$\phi$も徐々に大きくなり、クレーンが倒れ始めた。アームと球のみが風速$v$の風を受けるものとして、このときの$v$[m/s]の値を有効数字2桁で求めよ。

  $a=2.0$m、$m=1.0\times 10^4$kg、$M=4.0\times 10^4$kg、$b=0.60$m、$x=30.0$m、$L=4.5$m、$h=6.0$m、$z=15$m、$g=10.0$m/s²とする