$n$モルの単原子分子理想気体が絶対温度$T$、圧力$P$、体積$V$の状態にある。気体定数を$R$とすると、状態方程式は$\fbox{(1)数式}$、と表され、内部エネルギー$U$は$\fbox{(2)数式}$で与えられる。熱力学の$\fbox{(3)語句}$法則から、この気体の定圧モル比熱$C_p$は$\fbox{(4)数式}$であることが導かれる。

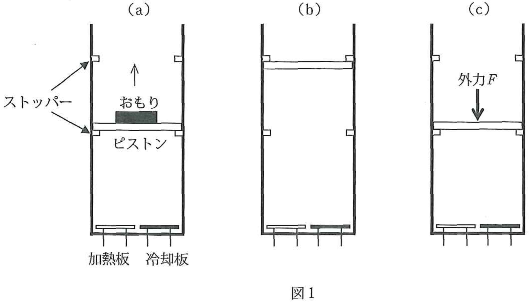
鉛直に向けたシリンダー内に$1$モルの単原子分子理想気体を閉じ込めた(図1)。断熱材で作られたピストンとシリンダーの間に摩擦はなく、ピストンは気体を密封したままシリンダー内を上下に滑らかに動くことができる。シリンダー内には加熱板と冷却板が取り付けてあり、内部の気体を一様にゆっくり加熱、冷却できる。加熱板と冷却板の熱容量は無視でき、加熱、冷却のとき以外は熱の出入りは遮断されている。ピストンの断面積は$S$で、ピストンの質量は無視できる。

最初、シリンダー内の気体の圧力は外部の大気圧$P_0$に等しく、ピストンは下のストッパーの位置にあり、内部に閉じ込められた気体の体積は$V_0$であった。ピストンの上に質量$M$のおもりを乗せ、加熱板が$Q_1$の熱量を発生したところで気体の温度が$T_1$となり、ピストンがゆっくり上昇を始めた(図1(a))。この瞬間を状態$\text{A}$とよぶ。状態$\text{A}$におけるシリンダー内の気体の圧力を$P_1=P_0+\Delta P$とする。

• 問1$\Delta P$を求めよ。
以下の問については、解答群から答えを選び番号で答えよ。
• 問2温度$T_1$、および熱量$Q_1$を求めよ。
状態$\text{A}$の後、加熱を再開したところ、ピストンがゆっくり上昇し、上のストッパーで停止した。この瞬間に加熱を止めた。このとき追加した熱量は$Q_2$であり、気体の体積は$2\dfrac{3}{5}V_0$であった(状態$\text{B}$とよぶ)。
• 問3状態$\text{B}$の気体の温度$T_2$と熱量$Q_2$を求めよ。
状態$\text{B}$の後、おもり$M$をはずしてゆっくり冷却を始めた(図1(b))。シリンダー内の気体から熱量$Q_3$を奪ったところでピストンが下がり始めたので、この瞬間に冷却を停止した(状態$\text{C}$とよぶ)。
• 問4状態$\text{C}$の気体の温度$T_3$、および熱量$Q_3$を求めよ。

次に、状態$\text{C}$で下向きの外力$F$を加え、ピストンを下のストッパーの位置までゆっくり押し込んだ(図1(c)、状態$\text{D}$とよぶ)。

• 問5状態$\text{D}$の気体の温度$T_4$を求めよ。ただし、状態$\text{C}$から状態$\text{D}$への変化に際しては、理想気体の状態方程式とともに、「$PV\dfrac{3}{5}=$一定」の関係が成り立つ。
解答群
• (1) $\dfrac{3}{5}\dfrac{P_0V_0}{R}$
• (2) $\dfrac{P_0V_0}{R}$
• (3) $\dfrac{2^\frac{3}{5}P_0V_0}{R}$
• (4) $\dfrac{2P_0V_0}{R}$
• (5) $\dfrac{2^\frac{5}{3}P_0V_0}{R}$
• (6) $\dfrac{3}{5}^\frac{(P_0+\Delta P)V_0}{R}$
• (7) $\dfrac{(P_0+\Delta P)V_0}{R}$
• (8) $\dfrac{2^\frac{3}{5}(P_0+\Delta P)V_0}{R}$
• (9) $\dfrac{2(P_0+\Delta P)V_0}{R}$
• (10) $\dfrac{2^\frac{5}{3}(P_0+\Delta P)V_0}{R}$
• (11) $\dfrac{3}{5}\dfrac{(P_0-\Delta P)V_0}{R}$
• (12) $\dfrac{(P_0-\Delta P)V_0}{R}$
• (13) $\dfrac{2^\frac{3}{5}(P_0-\Delta P)V_0}{R}$
• (14) $\dfrac{2(P_0-\Delta P)V_0}{R}$
• (15) $\dfrac{2^\frac{5}{3}(P_0-\Delta P)V_0}{R}$
• (16) $\Delta P\cdot V_0$
• (17) $\dfrac{3}{2}\Delta P\cdot V_0$
• (18) $\dfrac{5}{2}\Delta P\cdot V_0$
• (19) $2^\frac{3}{5}\Delta P\cdot V_0$
• (20) $\dfrac{3}{2}2^\frac{3}{5}\Delta P\cdot V_0$
• (21) $\dfrac{5}{2}2^\frac{3}{5}\Delta P\cdot V_0$
• (22) $(2^\frac{3}{5}-1)(P_0+\Delta P)V_0$
• (23) $\dfrac{3}{2}(2^\frac{3}{5}-1)(P_0+\Delta P)V_0$
• (24) $\dfrac{5}{2}(2^\frac{3}{5}-1)(P_0+\Delta P)V_0$
• (25) $(2^\frac{3}{5}+1)(P_0+\Delta P)V_0$
• (26) $\dfrac{3}{2}(2^\frac{3}{5}+1)(P_0+\Delta P)V_0$
• (27) $\dfrac{5}{2}(2^\frac{3}{5}+1)(P_0+\Delta P)V_0$
• (28) $(2^\frac{3}{5}-1)(P_0-\Delta P)V_0$
• (29) $\dfrac{3}{2}(2^\frac{3}{5}-1)(P_0-\Delta P)V_0$
• (30) $\dfrac{5}{2}(2^\frac{3}{5}-1)(P_0-\Delta P)V_0$