北里大学物理2013年第1問
次の問い(問1~問5)の空所四角に入る適語を解答詳から選択せよ。(解答番号$\fbox{1}$~$\fbox{14}$)
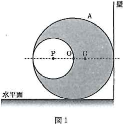
- 問1 図1のように、点$\text{O}$を中心とする半径$r$[m]で重さ$W$[N]の一様な円板から、点$\text{O}$からの距離が$\dfrac{r}{2}$の点$\text{P}$を中心とする半径$\dfrac{r}{3}$の円板をくりぬいた物体$\text{A}$がある。$\text{A}$の重心を点$\text{G}$とすると、$\text{OG}$間の距離は$\fbox{1}\times r$[m]である。点$\text{O}$と点$\text{P}$を通る直線が水平となり、あらい水平面と鉛直でなめらかな壁とに接するように$\text{A}$を置いたところ、$\text{A}$は静止した。このとき、$\text{A}$が水平面から受ける摩擦力の大きさは$\fbox{2}$[N]である。
解答群- (1) $\dfrac{1}{16}$
- (2) $\dfrac{1}{12}$
- (3) $\dfrac{1}{10}$
- (4) $\dfrac{1}{9}$
- (5) $\dfrac{1}{8}$
- (6) $\dfrac{1}{7}$
- (7) $\dfrac{1}{6}$
- (8) $\dfrac{1}{5}$
- (9) $\dfrac{1}{4}$
- (10) $\dfrac{1}{3}$
- (11) $\dfrac{3}{8}$
- (12) $\dfrac{2}{5}$
- (13) $\dfrac{1}{1}$
- (14) $\dfrac{3}{5}$
- (15) $\dfrac{2}{3}$
- (16) $\dfrac{3}{4}$
- (17) $1$
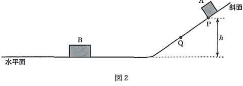
- 問2 図2のように、ともになめらかな水平面と斜面がなめらかにつながっている。水平面からの高さ$h$[m]の斜面上の点$\text{P}$から小物体$\text{A}$を静かに放したところ、$\text{A}$は斜面をすべり下り、水平面上にある$\text{A}$の4倍の質量をもつ小物体$\text{B}$と弾性衝突した。衝突後、$\text{A}$は点$\text{Q}$まで斜面を上った後、ふたたび斜面をすべり下りた。衝突直後の$\text{B}$の速さは$\fbox{3}$[m/s]であり、点$\text{Q}$の水平面からの高さは$\fbox{4}$[m]である。ただし、重力加速度の大きさを$g$[m/s2]とし、すべての運動は同じ鉛直面内で起こるものとする。
$\fbox{3}$の解答群- (1) $\dfrac{\sqrt{gh}}{5}$
- (2) $\dfrac{\sqrt{2gh}}{5}$
- (3) $\dfrac{\sqrt{gh}}{3}$
- (4) $\dfrac{\sqrt{3gh}}{5}$
- (5) $\dfrac{2\sqrt{gh}}{5}$
- (6) $\dfrac{\sqrt{2gh}}{3}$
- (7) $\dfrac{2\sqrt{2gh}}{5}$
- (8) $\dfrac{\sqrt{3gh}}{3}$
- (9) $\dfrac{3\sqrt{gh}}{5}$
- (10) $\dfrac{2\sqrt{gh}}{3}$
- (11) $\dfrac{2\sqrt{2gh}}{3}$
- (12) $\sqrt{gh}$
- (13) $\dfrac{3\sqrt{3gh}}{5}$
- (14) $\sqrt{2gh}$
- (15) $\sqrt{3gh}$
- (1) $\dfrac{1}{36}h$
- (2) $\dfrac{1}{25}h$
- (3) $\dfrac{1}{16}h$
- (4) $\dfrac{1}{9}h$
- (5) $\dfrac{4}{25}h$
- (6) $\dfrac{1}{4}h$
- (7) $\dfrac{25}{9}h$
- (8) $\dfrac{4}{9}h$
- (9) $\dfrac{9}{16}h$
- (10) $\dfrac{16}{25}h$
- (11) $\dfrac{25}{36}h$
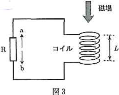
- 問3 図3のように、断面積$S$[m2]、長さ$L$[m]、巻き数が長さ1m当たり$N$[回/m]のコイルを、抵抗値$R$[\Omega]の電気抵抗$\text{R}$に接続し、コイルの断面を垂直につらぬくように、図の矢印の向きに一様な磁場を加えた。この磁場の磁束密度の大きさを1秒間に$\Delta B$[T]ずつ増加させたとき、コイルに生じる誘導起電力の大きさは$\fbox{5}$[V]であり、$\text{R}$を流れる電流は$\fbox{6}$の向きに大きさ$\fbox{7}$[A]である。
$\fbox{5}$の解答群- (1) $\Delta B$
- (2) $\Delta B\cdot S$
- (3) $\Delta B\cdot N$
- (4) $\Delta B\cdot NS$
- (5) $\Delta B\cdot LNS$
- (6) $\dfrac{\Delta B}{L}$
- (7) $\dfrac{\Delta B\cdot S}{L}$
- (8) $\dfrac{\Delta B\cdot NS}{L}$
- (9) $\dfrac{\Delta B}{S}$
- (10) $\dfrac{\Delta B\cdot N}{S}$
- (11) $\dfrac{\Delta B\cdot NL}{S}$
- (1) $a$
- (2) $b$
- (1) $\dfrac{\Delta B}{R}$
- (2) $\dfrac{\Delta B\cdot S}{R}$
- (3) $\dfrac{\Delta B\cdot N}{R}$
- (4) $\dfrac{\Delta B\cdot NS}{R}$
- (5) $\dfrac{\Delta B\cdot LNS}{R}$
- (6) $\dfrac{\Delta B}{LR}$
- (7) $\dfrac{\Delta B\cdot S}{LR}$
- (8) $\dfrac{\Delta B\cdot NS}{LR}$
- (9) $\dfrac{\Delta B}{SR}$
- (10) $\dfrac{\Delta B\cdot N}{SR}$
- (11) $\dfrac{\Delta B\cdot NL}{SR}$
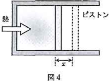
- 問4 図4のように、なめらかに動く断面積$S$[m2]のピストンのついた断熱容器に単原子分子理想気体を封入したところ、気体の圧力は外気圧$P$[Pa]とつり合ってピストンは静止した。つぎに、気体に外部から熱を加えたところ気体は膨張し、ピストンは$x$[m]移動した。この移動により、気体が外部にした仕事は$\fbox{8}\times\fbox{9}$[J]であり、気体の内部工ネルキーの増加は$\fbox{10}\times\fbox{11}$[J]である。また、気体に加えた熱量は$\fbox{12}\times\fbox{13}$[J]である。
$\fbox{8}$と$\fbox{10}$と$\fbox{12}$の解答群- (1) $\dfrac{1}{5}$
- (2) $\dfrac{1}{3}$
- (3) $\dfrac{2}{5}$
- (4) $\dfrac{1}{2}$
- (5) $\dfrac{2}{3}$
- (6) $1$
- (7) $\dfrac{3}{2}$
- (8) $2$
- (9) $\dfrac{5}{2}$
- (10) $3$
- (11) $\dfrac{7}{2}$
- (12) $4$
- (13) $\dfrac{9}{2}$
- (14) $5$
- (1) $Sx$
- (2) $PS$
- (3) $Px$
- (4) $PSx$
- (5) $\dfrac{Px}{S}$
- (6) $\dfrac{Sx}{P}$
- (7) $\dfrac{PS}{x}$
- (8) $\dfrac{1}{PSx}$
- (9) $\dfrac{S}{Px}$
- (10) $\dfrac{P}{Sx}$
- (11) $\dfrac{x}{PS}$
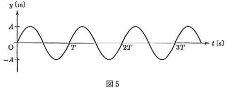
- 問5 図5は$x$軸上を正の向きに進む振幅$A$[m]、波長$\lambda$[m]、周期$T$[s]の正磁波の、原点における時刻$t$[s]と変位$y$[m]との関係をグラフに表したものである。この波の時刻$\dfrac{T}{2}$、$x$軸上の位置$\dfrac{7\lambda}{8}$での変位は$\fbox{14}$[m]である。
解答群- (1) $-A$
- (2) $-\dfrac{\sqrt{3}A}{2}$
- (3) $-\dfrac{3A}{4}$
- (4) $-\dfrac{\sqrt{2}A}{2}$
- (5) $-\dfrac{A}{2}$
- (6) $-\dfrac{A}{4}$
- (7) $0$
- (8) $\dfrac{A}{4}$
- (9) $\dfrac{A}{2}$
- (10) $\dfrac{\sqrt{2}A}{3}$
- (11) $\dfrac{3A}{4}$
- (12) $\dfrac{\sqrt{3}A}{2}$
- (13) $A$