北里大学物理2013年第2問
次の問い(問1~問6)の空所四角に入る適語を解答群から選択せよ。(解答番号$\fbox{15}$~$\fbox{22}$)
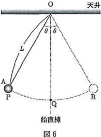
図6のように、一端を天井の点$\text{O}$に固定した長さ$L$[m]の軽い糸の他端に、質量$m$[kg]の小物体$\text{A}$を取りつけた。糸がたるまないようにして、糸と船直線のなす角が$\theta$[rad]となる点$\text{P}$で$\text{A}$を静かに放したところ、$\text{A}$は点$\text{O}$の真下の点$\text{Q}$を通過後、点$\text{P}$と同じ高さの点$\text{R}$に達した。ただし、重力加速度の大きさを$g$[m/s2]とし、点$\text{Q}$を重力による位置エネルギーの基準点とする。

- 問1 $\text{A}$が点$\text{P}$の位置にあるとき、$\text{A}$の重力による位置エネルギーは$\fbox{15}$[J]である。
解答群- (1) $mgL$
- (2) $mgL\sin\theta$
- (3) $mgL\cos\theta$
- (4) $mgL\tan\theta$
- (5) $\dfrac{mgL}{\sin\theta}$
- (6) $\dfrac{mgL}{\cos\theta}$
- (7) $\dfrac{mgL}{\tan\theta}$
- (8) $mgL(1-\sin\theta)$
- (9) $mgL(1-\cos\theta)$
- (10) $mgL(1-\tan\theta)$
- 問2 点$\text{Q}$での$\text{A}$の速さは$\fbox{16}$[m/s]である。また、このときの糸の張力の大きさは$\fbox{17}$Nである。
$\fbox{16}$の解答群- (1) $\sqrt{gL}$
- (2) $\sqrt{gL\sin\theta}$
- (3) $\sqrt{gL\cos\theta}$
- (4) $\sqrt{gL\tan\theta}$
- (5) $\sqrt{gL\sin\theta\cos\theta}$
- (6) $\sqrt{gL\sin\theta\tan\theta}$
- (7) $\sqrt{2gL}$
- (8) $\sqrt{2gL\sin\theta}$
- (9) $\sqrt{2gL\cos\theta}$
- (10) $\sqrt{2gL\tan\theta}$
- (11) $\sqrt{2gL\sin\theta\cos\theta}$
- (12) $\sqrt{2gL\sin\theta\tan\theta}$
- (13) $\sqrt{\dfrac{2gL}{\sin\theta}}$
- (14) $\sqrt{\dfrac{2gL}{\cos\theta}}$
- (15) $\sqrt{\dfrac{2gL}{\tan\theta}}$
- (16) $\sqrt{2gL(1-\sin\theta)}$
- (17) $\sqrt{2gL(1-\cos\theta)}$
- (18) $\sqrt{2gL(1-\tan\theta)}$
- (1) $mg$
- (2) $2mg$
- (3) $3mg$
- (4) $mg\sin\theta$
- (5) $mg\cos\theta$
- (6) $mg\tan\theta$
- (7) $mg(2-\sin\theta)$
- (8) $mg(2-\cos\theta)$
- (9) $mg(2-\tan\theta)$
- (10) $\dfrac{mg}{\sin\theta}$
- (11) $\dfrac{mg}{\cos\theta}$
- (12) $\dfrac{mg}{\tan\theta}$
- (13) $mg(3-2\sin\theta)$
- (14) $mg(3-2\cos\theta)$
- (15) $mg(3-2\tan\theta)$
- 問3 $\text{B}$が$\text{A}$に衝突した直後の、$\text{A}$の速さは$\fbox{18}$[m/s]であり、$\fbox{B}$の速さは$\fbox{19}$[m/s]である。
解答群- (1) $0$
- (2) $\dfrac{1}{6}$
- (3) $\dfrac{1}{3}$
- (4) $\dfrac{1}{2}$
- (5) $\dfrac{2}{3}$
- (6) $\dfrac{5}{6}$
- (7) $1$
- (8) $\dfrac{7}{6}$
- (9) $\dfrac{4}{3}$
- (10) $\dfrac{3}{5}$
- (11) $\dfrac{11}{6}$
- (12) $2$
- 問4 $\text{A}$が円連動しているとき、糸の張力の大きさを$m$、$g$、$\theta$を用いて表すと$\fbox{20}$[N]である
解答群- (1) $mg$
- (2) $2mg$
- (3) $3mg$
- (4) $mg\sin\theta$
- (5) $mg\cos\theta$
- (6) $mg\tan\theta$
- (7) $mg(2-\sin\theta)$
- (8) $mg(2-\cos\theta)$
- (9) $mg(2-\tan\theta)$
- (10) $\dfrac{mg}{\sin\theta}$
- (11) $\dfrac{mg}{\cos\theta}$
- (12) $\dfrac{mg}{\tan\theta}$
- (13) $mg(3-2\sin\theta)$
- (14) $mg(3-2\cos\theta)$
- (15) $mg(3-2\tan\theta)$
- 問5 $\text{A}$が円連動していることから、$\text{B}$の衝突前の速さ$v$を$g$、$L$、$\theta$を用いて表すと$\fbox{21}$[m/s]である。
解答群- (1) $\sqrt{2gL}$
- (2) $\sqrt{2gL\sin\theta}$
- (3) $\sqrt{2gL\cos\theta}$
- (4) $\sqrt{2gL\tan\theta}$
- (5) $\sqrt{2gL\sin\theta\cos\theta}$
- (6) $\sqrt{2gL\sin\theta\tan\theta}$
- (7) $\dfrac{3}{2}\sqrt{gL}$
- (8) $\dfrac{3}{2}\sqrt{gL\sin\theta}$
- (9) $\dfrac{3}{2}\sqrt{gL\cos\theta}$
- (10) $\dfrac{3}{2}\sqrt{gL\tan\theta}$
- (11) $\dfrac{3}{2}\sqrt{gL\sin\theta\cos\theta}$
- (12) $\dfrac{3}{2}\sqrt{gL\sin\theta\tan\theta}$
- (13) $\sqrt{\dfrac{2gL}{\sin\theta}}$
- (14) $\sqrt{\dfrac{2gL}{\cos\theta}}$
- (15) $\sqrt{\dfrac{2gL}{\tan\theta}}$
- (16) $\sqrt{2gL(1-\sin\theta)}$
- (17) $\sqrt{2gL(1-\cos\theta)}$
- (18) $\sqrt{2gL(1-\tan\theta)}$
- 問6 $\text{A}$の円連動の周期を$g$、$L$、$\theta$を用いて表すと$\fbox{22}$[s]である。
解答群- (1) $\dfrac{\pi}{2}\sqrt{\dfrac{L}{g\sin\theta}}$
- (2) $\dfrac{\pi}{2}\sqrt{\dfrac{L}{g\cos\theta}}$
- (3) $\dfrac{\pi}{2}\sqrt{\dfrac{L}{g}}$
- (4) $\dfrac{\pi}{2}\sqrt{\dfrac{L\sin\theta}{g}}$
- (5) $\dfrac{\pi}{2}\sqrt{\dfrac{L\cos\theta}{g}}$
- (6) $\pi\sqrt{\dfrac{L}{g\sin\theta}}$
- (7) $\pi\sqrt{\dfrac{L}{g\cos\theta}}$
- (8) $\pi\sqrt{\dfrac{L}{g}}$
- (9) $\pi\sqrt{\dfrac{L\sin\theta}{g}}$
- (10) $\pi\sqrt{\dfrac{L\cos\theta}{g}}$
- (11) $2\pi\sqrt{\dfrac{L}{g\sin\theta}}$
- (12) $2\pi\sqrt{\dfrac{L}{g\cos\theta}}$
- (13) $2\pi\sqrt{\dfrac{L}{g}}$
- (14) $2\pi\sqrt{\dfrac{L\sin\theta}{g}}$
- (15) $2\pi\sqrt{\dfrac{L\cos\theta}{g}}$
つぎに、$\text{A}$が点$\text{R}$の位置に達した瞬間に、質量$\dfrac{1}{2}$[kg]の小物体$\text{B}$を、$\text{A}$の運動する鉛直面と垂直に速さ$v$[m/s]で$\text{A}$と弾性衡実させたところ、図7のように$\text{A}$は糸と鉛直線のなす角$\theta$[rad]を一定に保ったまま水平面内を円運動した。