北里大学物理2012年第1問
次の問い(1~5)の空所$\fbox{ }$に入る適語を解答群から選択せよ。$\big($解答番号$\fbox{1}$~$\fbox{21}\big)$
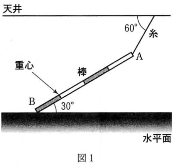
- 図1のように、重さ$W$[N]の細い棒の端点Aに軽い糸をつけて天井からつり下げ、もう一方の端点Bがあらい水平面と接するように静かに置いたところ、糸は天井となす角$60^\circ$で、棒は水平面となす角$30^\circ$となって静止した。このとき、糸の張力の大きさは$\fbox{1}\times{W}$[N]である。ただし、棒の重心は、端点Aから棒の長さの4分の3だけ離れた位置である。
解答群
- (1) $\dfrac{\sqrt{3}}{8}$
- (2) $\dfrac{1}{4}$
- (3) $\dfrac{\sqrt{3}}{6}$
- (4) $\dfrac{1}{3}$
- (5) $\dfrac{\sqrt{3}}{4}$
- (6) $\dfrac{1}{2}$
- (7) $\dfrac{\sqrt{3}}{3}$
- (8) $\dfrac{3\sqrt{3}}{8}$
- (9) $\dfrac{3}{4}$
- (10) $\dfrac{\sqrt{3}}{2}$
- (11) $1$
- (12) $\dfrac{2\sqrt{3}}{3}$
- (13) $\dfrac{3\sqrt{3}}{3}$
- (14) $\sqrt{3}$
- 地球を半径$R$[m]の球体であるとすると、地球の表面から小物体$\text{A}$が無限のかなたへ飛んでいくには、地表での重力加速度の大きさを$g$$[\text{m}/\text{s}^2]$として、少なくとも$\text{A}$に$\fbox{2}\times\sqrt{gR}$[m/s]の初速度を地表で与えなければならない。また、$\text{A}$の初速度が$\fbox{2}\times\sqrt{gR}$[m/s]の$\dfrac{1}{2}$の場合、$\text{A}$は地球の中心から最大で$\fbox{3}\times{R}$[m]だけしか離れることができない。ただし、地球の重力以外の影響は考えないものとする。
$\fbox{2}$の解答群
- (1) $\dfrac{1}{2\sqrt{2}}$
- (2) $\dfrac{1}{2}$
- (3) $\dfrac{1}{\sqrt{2}}$
- (4) $1$
- (5) $\sqrt{2}$
- (6) $2$
- (7) $2\sqrt{2}$
- (8) $\dfrac{1}{2\sqrt{2\pi}}$
- (9) $\dfrac{1}{2\sqrt{\pi}}$
- (10) $\dfrac{1}{\sqrt{2\pi}}$
- (11) $\sqrt{\pi}$
- (12) $\sqrt{2\pi}$
- (13) $2\sqrt{\pi}$
- (14) $2\sqrt{2\pi}$
- (1) $\dfrac{4}{3}$
- (2) $\dfrac{3}{2}$
- (3) $\dfrac{5}{3}$
- (4) $2$
- (5) $\dfrac{7}{3}$
- (6) $\dfrac{5}{2}$
- (7) $\dfrac{8}{3}$
- (8) $3$
- (9) $\dfrac{10}{3}$
- (10) $\dfrac{7}{2}$
- (11) $\dfrac{11}{3}$
- (12) $4$
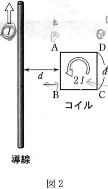
- 図2のように、真空中で細く長いまっすぐな導線と1辺が$d$[m]の正方形のコイル$\text{ABCD}$が同じ平面内に置かれており、導線とコイルの辺$\text{AB}$は平行で距離$d$だけ離れている。導線には矢印の向きに電流$I$[A]が流れており、コイルには2$I$[A]の電流が$\text{A}\rightarrow\text{B}\rightarrow\text{C}\rightarrow\text{D}\rightarrow\text{A}$の向きに流れている。このとき、コイルは導線を流れる電流により、全体として$\fbox{4}$に大きさ$\fbox{5}$[N]の力を受ける。ただし、真空の透磁率を$\mu_0[\text{N}/\text{A}^2]$とする。
$\fbox{4}$の解答群
- (1) 導線を流れる電流と同じ向き
- (2) 導線を流れる電流と反対向き
- (3) 導線とコイルが反発する向き
- (4) 導線とコイルが引きあう向き
- (5) 紙面の奥から手前向き
- (6) 紙面の手前から奥向き
- (1) $\dfrac{\mu_0I^2}{4\pi{d}}$
- (2) $\dfrac{\mu_0I^2}{2\pi{d}}$
- (3) $\dfrac{\mu_0I^2}{\pi{d}}$
- (4) $\dfrac{2\mu_0I^2}{\pi{d}}$
- (5) $\dfrac{4\mu_0I^2}{\pi{d}}$
- (6) $\dfrac{\mu_0I^2}{4\pi}$
- (7) $\dfrac{\mu_0I^2}{2\pi}$
- (8) $\dfrac{\mu_0I^2}{\pi}$
- (9) $\dfrac{2\mu_0I^2}{\pi}$
- (10) $\dfrac{4\mu_0I^2}{\pi}$
- (11) $\dfrac{\mu_0I^2d}{4\pi}$
- (12) $\dfrac{\mu_0I^2d}{2\pi}$
- (13) $\dfrac{\mu_0I^2d}{\pi}$
- (14) $\dfrac{2\mu_0I^2d}{\pi}$
- (15) $\dfrac{4\mu_0I^2d}{\pi}$
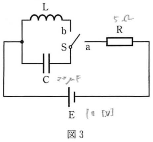
- 図3のように、抵抗値5.0$[\omega]$の電気抵抗R、電気容量20$\mu$[F]のコンデンサー$\text{C}$、自己インダクタンス5.0 [H]のコイル$\text{L}$、内部抵抗が無視できる起電力10 [V]の直流電源$\text{E}$、およびスイッチ$\text{S}$からなる回路がある。$\text{S}$を接点$\text{a}$に接続した直後に$\text{R}$に流れる電流は$\fbox{6}.\fbox{7}$[A]であり、じゅうぶんに時間が経過した後に$\text{C}$にたくわえられている電気量は$\fbox{8}.\fbox{9}\times10^{\fbox{10}\fbox{11}}$[C]である。つぎに、$\text{S}$を接点$\text{a}$から接点$\text{b}$に切り替えたところ、$\text{L}$と$\text{C}$の間に振動電流が流れた。このとき、流れる電流の大きさの最大値は$\fbox{12}.\fbox{13}\times10^{\fbox{14}\fbox{15}}$[A]である。ただし、はじめ$\text{S}$はどこにも接しておらず、$\text{C}$には電荷はたくわえられていないものとする。また、有効数字は2桁とする。
$\fbox{10}$と$\fbox{14}$の解答群
- (1) +
- (2) -
- (1) 1
- (2) 2
- (3) 3
- (4) 4
- (5) 5
- (6) 6
- (7) 7
- (8) 8
- (9) 9
- (10) 0
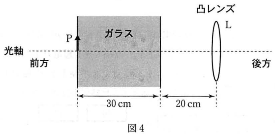
- 図4のように、焦点距離24 [cm]の凸レンズ$\text{L}$の前方20 [cm]の位置に、厚さ30 [cm]で屈折率1.5の透明なガラスの板を光軸と垂直になるように置いた。細い物体$\text{P}$を、光軸上でガラスの前方側の面上に置くと$\text{L}$の後方$\fbox{16}.\fbox{17}\times10^{\fbox{18}\fbox{19}}$[cm]の位置に倍率$\fbox{6}.\fbox{7}$倍の$\text{P}$の実像ができる。ただし、有効数字は2桁とする。
$\fbox{10}$と$\fbox{14}$の解答群
- (1) +
- (1) -
- (1) 1
- (2) 2
- (3) 3
- (4) 4
- (5) 5
- (6) 6
- (7) 7
- (8) 8
- (9) 9
- (10) 0