真空中で以下の実験を行った。物理量はSI国際単位系を用いてあるとして、以下の問に答えなさい。真空の透磁率を$\mu_0$、誘電率を$\epsilon_0$とする。

• (1) 単位長さあたり$n$回巻かれた、長さ$a$、断面の半径が$r$であるソレノイドコイルがある。このソレノイドコイルに電流$I$を流すと、作られるコイル内の磁場は一様でその磁束密度は$\mu_0nI$であることが知られている。$\Delta t$時間に、$\Delta I$の電流が増加したとき、磁束$\Phi$の単位時問当たりの変化の割合$\Delta\Phi/\Delta t$はいくらか。その結果このコイルの両端に生じる起電力はいくらか。一般に、自己インダクタンス$L$は群導起電力$V$、電流の時間変化の割合$\Delta I/\Delta t$とどのような関係で結び付けられているか。これを用いるとこのコイルの自己インダクタンス$L$はどう表現されるか。
• (2) 面積$S$の2枚の導板を距離$d$だけ離して平行板コンデンサーを作った。電池をつなぎ両極板間に電位差$E$を与えた。しばらく放置した後、電池を外した。蓄えられている電気量はいくらか。
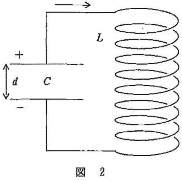
• (3) (2)の電荷を蓄えたコンデンサーの電気容量を$C$であらわす。このコンデンサーを図2のように自己インダクタンス$L$のコイルとつないだ。図中、コンデンサーに表現されている$+-$は、初めに蓄えた電荷の符号である。回路を流れる電流は特徴的な時間変化を示した。この回路に流れる電流の時間変化の様子を、回路をつないだ時を$t=0$として、解答欄に書き入れなさい。ただし図2中の矢印の方向を正とする。コイルに蓄えられているエネルギーの時間変化も解答欄の図に書きなさい。図には特徴的な値(矢印の位置)を横軸、縦軸に記入すること。