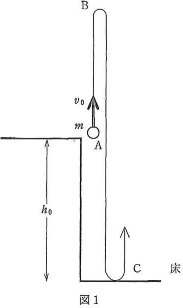
図1に示すように、床から高さ$h_0$の位置$\text{A}$から、質量$m$の小物体を鉛直上方に速さ$v_0$で投げ上げる。小物体は最高点$\text{B}$に達し、そのまま、床($\text{C}$点)に落下し、はね返るものとする。床とのはねかえり係数を$e(0\lt e\lt 1)$、重力加速度の大きさを$g$とし、以下の、各問に答えよ。ただし、小物体の大きさや空気の抵抗は無視できるとする。

• 問1 投げられてから最高点$\text{B}$に達するまでの時間は$\fbox{1}$であり、そのときの速さは$\fbox{2}$である。また、最高点の床からの高さは$\fbox{3}$である。
  • (1) $\fbox{1}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $0$
    • (b) $\dfrac{1}{2}gv_0$
    • (c) $gv_0$
    • (d) $\dfrac{g}{v_0}$
    • (e) $\dfrac{g}{2v_0}$
    • (f) $\dfrac{v_0}{g}$
    • (g) $\dfrac{v_0}{2g}$
    • (h) $\dfrac{{v_0}^2}{g}$
    • (i) $\dfrac{{v_0}^2}{2g}$
  • (2) $\fbox{2}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $0$
    • (b) $v_0$
    • (c) $\dfrac{1}{2}v_0$
    • (d) $\dfrac{v_0}{g}$
    • (e) $\dfrac{v_0}{2g}$
    • (f) $\dfrac{{v_0}^2}{g}$
    • (g) $\dfrac{{v_0}^2}{2g}$
    • (h) $\dfrac{2{v_0}^2}{g}$
  • (3) $\fbox{3}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $h_0$
    • (b) $\dfrac{v_0}{g}$
    • (c) $\dfrac{v_0}{2g}$
    • (d) $\dfrac{{v_0}^2}{g}$
    • (e) $\dfrac{{v_0}^2}{2g}$
    • (f) $h_0+\dfrac{v_0}{g}$
    • (g) $h_0+\dfrac{v_0}{2g}$
    • (h) $h_0+\dfrac{{v_0}^2}{g}$
    • (i) $h_0+\dfrac{{v_0}^2}{2g}$
• 問2 小物体が最高点$\text{B}$から床の$\text{C}$点に達するまでの時間は$\fbox{4}$であり、$\text{C}$点に達したときの速さは$\fbox{5}$である。この速さで小物体は床の$\text{C}$点に衝突し、はね返りの運動をはじめる。
  • (1) $\fbox{4}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $\dfrac{v_0}{g}$
    • (b) $\dfrac{v_0}{2g}$
    • (c) $\dfrac{v_0}{g}+\dfrac{h_0}{v_0}$
    • (d) $\sqrt{\dfrac{h_0}{g}}$
    • (e) $\sqrt{\dfrac{2h_0}{g}}$
    • (f) $\dfrac{\sqrt{{v_0}^2+2h_0}}{g}$
    • (g) $\dfrac{\sqrt{{v_0}^2+2v_0}}{g}$
    • (h) $\dfrac{\sqrt{{v_0}^2+2gh_0}}{g}$
    • (i) $\dfrac{\sqrt{{v_0}^2+2mg}}{g}$
  • (2) $\fbox{5}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $2v_0$
    • (b) $v_0+gh_0$
    • (c) $v_0+\dfrac{h_0}{v_0}$
    • (d) $\sqrt{2gh_0}$
    • (e) $\sqrt{{v_0}^2+2gh_0}$
    • (f) $\sqrt{{v_0}^2+gh_0}$
    • (g) $\sqrt{{v_0}^2+\dfrac{gh_0}{2}}$
    • (h) $\sqrt{{v_0}^2+2mgh_0}$
    • (i) $\sqrt{{v_0}^2+mgh_0}$
• 問3小物体は$\text{C}$点ではね返りの運動をくり返すが、1回目にはね返った直後の速さは$\fbox{6}$である。また、2回目にはね返った直後の速さは$\fbox{7}$である。ただし、今後は$\text{B}$点の床からの高さを$H$として答えよ。
  • (1) $\fbox{6}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $ev_0$
    • (b) $2ev_0$
    • (c) $e\sqrt{gH}$
    • (d) $e\sqrt{2gH}$
    • (e) $egH$
    • (f) $2egH$
    • (g) $\dfrac{\sqrt{gH}}{e}$
    • (h) $\dfrac{\sqrt{2gH}}{e}$
    • (i) $\dfrac{2gH}{e}$
  • (2) $\fbox{7}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $(1+e)v_0$
    • (b) $2(1+e)v_0$
    • (c) $(1+e)\sqrt{2gH}$
    • (d) $(1+e)^2\sqrt{2gH}$
    • (e) $2(1+e)gH$
    • (f) $2e^2gH$
    • (g) $e^2\sqrt{gH}$
    • (h) $e^2\sqrt{2gH}$
    • (i) $2e^2\sqrt{2gH}$
• 問4 小物体が$\text{C}$点で1回目にはね上がった時から2回目のはね上がりまでの時間は$\fbox{8}$である。
  $\fbox{8}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
  • (a) $e\dfrac{2H}{g}$
  • (b) $2e\dfrac{2H}{g}$
  • (c) $e\dfrac{H}{g}$
  • (d) $2e\dfrac{H}{g}$
  • (e) $e\dfrac{H}{2g}$
  • (f) $2e\dfrac{2H}{2g}$
  • (g) $e^2frac{2H}{g}$
  • (h) $2e^2\dfrac{2H}{g}$
  • (i) $(1+e)\dfrac{2H}{g}$
• 問5 小物体が$\text{B}$点を通過してから、$\text{C}$点でのはねかえりの運動がなくなるまでの時問は$\fbox{9}$である。
  $\fbox{9}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
  • (a) $\dfrac{1}{1-e}\sqrt{\dfrac{2H}{g}}$
  • (b) $(1+e)\sqrt{\dfrac{2H}{g}}$
  • (c) $\dfrac{1-e}{1+e}\sqrt{\dfrac{2H}{g}}$
  • (d) $\dfrac{1+e}{1-e}\sqrt{\dfrac{2H}{g}}$
  • (e) $(1-e)\sqrt{\dfrac{2H}{g}}$
  • (f) $\dfrac{1}{1+e}\sqrt{\dfrac{2H}{g}}$
  • (g) $(1-e)\sqrt{\dfrac{H}{g}}$
  • (h) $\dfrac{1+e}{1-e}\sqrt{\dfrac{H}{g}}$
  • (i) $\dfrac{1-e}{1+e}\sqrt{\dfrac{H}{g}}$
• 問6 小物体が1回目のはねかえりで床面から受けた力積の大きさは$\fbox{10}$である。また、2回目のはねかえりで床面から受けた力積の大きさは$\fbox{11}$である。
  • (1) $\fbox{10}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $2m\sqrt{2gH}$
    • (b) $2em\sqrt{2gH}$
    • (c) $(1+e)m\sqrt{2gH}$
    • (d) $(1-e)m\sqrt{2gH}$
    • (e) $2(1+e)m\sqrt{2gH}$
    • (f) $2(1-e)m\sqrt{2gH}$
    • (g) $\dfrac{m\sqrt{2gH}}{2e}$
    • (h) $\dfrac{m\sqrt{2gH}}{1+e}$
    • (i) $\dfrac{m\sqrt{2gH}}{1-e}$
  • (2) $\fbox{11}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $2(1+e)m\sqrt{2gH}$
    • (b) $2e(1+e)m\sqrt{2gH}$
    • (c) $(1+e)^2m\sqrt{2gH}$
    • (d) $2em\sqrt{2gH}$
    • (e) $2e^2m\sqrt{2gH}$
    • (f) $e(1+e)m\sqrt{2gH}$
    • (g) $\dfrac{m\sqrt{2gH}}{2e^2}$
    • (h) $\dfrac{m\sqrt{2gH}}{e(1+e)}$
    • (i) $\dfrac{m\sqrt{2gH}}{(1+e)(1-e)}$
• 問7 床面が物体のはねかえりで受けた力積の合計の大きさは$\fbox{12}$である。
  $\fbox{12}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
  • (a) $m\sqrt{2gH}$
  • (b) $em\sqrt{2gH}$
  • (c) $(1-e)m\sqrt{2gH}$
  • (d) $(1+e)m\sqrt{2gH}$
  • (e) $\dfrac{1+e}{1-e}m\sqrt{2gH}$
  • (f) $(1-e^2)\sqrt{2gH}$
  • (g) $(1-e)^2\sqrt{2gH}$
  • (h) $(1+e)^2\sqrt{2gH}$
  • (i) $\dfrac{(1-e^2)}{2}m\sqrt{2gH}$
• 問8 小物体が$\text{B}$点を通過してから、$\text{C}$点でのはねかえりの運動がなくなるまでの間に、床面が小物体から受けた平均の力の大きさは、$\fbox{12}$を$\fbox{9}$で割ることによって求めることができる。
  その値は$\fbox{13}$である。$\fbox{13}$に入る式として最も通切なものを、次の(a)～(i)のうちから1つ選べ。
  • (a) $mg$
  • (b) $2mg$
  • (c) $\sqrt{2}mg$
  • (d) $\sqrt{3}mg$
  • (e) $\sqrt{5}mg$
  • (f) $emg$
  • (g) $(1-e)mg$
  • (h) $(1-e^2)mg$
  • (i) $\dfrac{(1-e^2)}{2}mg$