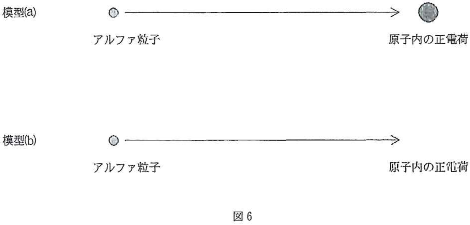
20世紀初頭、原子について次のことが明らかになって来た。原子の中には、元素の種類によって決まる一定個数の電子がある。電子は負電荷を持ち、質量は原子に比べて非常に小さい。一方、原子は中性だから、原子の中には、大きな質量を持つ正の電荷が存在していることになる。これらのことから、正電荷は原子の中にどのように分布しているのかが大きな問題になった。正電荷が原子の中心付近に集中しているとする模型(a)や原子全体に広がっているとする模型(b)が考えられた。このような原子に、アルファ粒子を当てたときどのように跳ね返るかを考えて見よう。アルファ粒子は正電荷$2e$($e$は電気素量)を持ち、電子よりはるかに大きい質量($m$とする)を持つ。原子の質量はアルファ粒子よりさらに大きいものとする。一般に重いものと軽いものが衝突すると、エネルギーと運動量の保存の法則により、軽いものは大きく跳ね飛ばされるが、重いものの進路はあまり変わらない。従って、アルファ粒子の進路は$\fbox{32}$と思われるので、原子内の$\fbox{33}$の分布についての情報が得られると期待される。

簡単のため、正電荷$Q$は半径$R$の球の中に一様に分布しているものとし、アルファ粒子がこれに正面衝突する場合を考えよう(図6)。電子の負電荷の影響は無視する。原子はアルファ粒子よりはるかに重く、アルファ粒子が衝突してもほとんど動かないものとする。球の中心からのアルファ粒子までの距離を$r$とする。真空中で距離$r$だけ離れた2つの電荷、$q$、$q’$の間に働く電気力は$F=k_0qq’/r^2$で与えられる。ここで、$k_0$は比例定数である。球状の電荷分布からの電気力は、球の中心にある点電荷からの力と同じである。従って、アルファ粒子に働く反発力の大きさは$\fbox{34}$に等しい。位置エネルギーの基準を$r=\infty$にとれば、アルファ粒子の持つ位置エネルギーは$\fbox{35}$となる。$r=\infty$の位置でのアルファ粒子の運動エネルギーを$E_0$とすると、距離$r$の位置での速さは$\fbox{36}$と表される。$R$が十分小さければ、$r\gt R$のうちに速さが$0$になり、反発力により後戻りし、$r=\infty$に向かって飛び去る。速さが$0$になるのは$r=\fbox{37}$のときである。従って、半径$R$が$\fbox{37}$より$\fbox{38}$ときはアルファ粒子は原子内の正電荷からの電気的反発力によって跳ね返される。

これに対し、$R$が大きいと、$r=R$になってもアルファ粒子の速さが$0$にならず、正電荷の球の中に突入する。すると、アルファ粒子は前方に分布する正電荷からは後ろ向きの反発力を受けるが、後方の正電荷からは前向きの反発力を受けることになり、全体としての反発力は弱くなる。電気力線の考えを使うと$r\lt R$でアルファ粒子に働く力は、半径$r$の球の内部の電荷が球の中心にある場合と同じであることが分かる。即ち、$r\lt R$での力の大きさは$F=2k_0eQr/R^3$となり、$r$に比例することが分かる。このことは、ばねの力と同じで、ばね定数が$k=-2k_0eQ/R^3$の場合に相当する(反発力なので$k$が負になっていることに注意)。従って、$r=0$を基準とする位置エネルギーは$kr^2/2=\fbox{39}$となり、その$r=R$(球の表面)における値は$\fbox{40}$となる。一方$\fbox{35}$の$r=R$(球の表面)における値は$\fbox{41}$となる。$r=\infty$を基準とし、球内外の位置エネルギーが$r=R$の位置で一致するようにするには、球内での位置エネルギーを$\fbox{39}+\fbox{42}$とすればよい。従って、$E_0\gt \fbox{42}$の場合はアルファ粒子が球の中心$r=0$の位置に達してもまだ運動エネルギーを持っており、ここを通過して前方に飛び去る。即ち原子は$E_0\gt\fbox{42}$のアルファ粒子を跳ね返せない。逆に言えば半径$R$が$\fbox{43}$より$\fbox{44}$ときはアルファ粒子は跳ね返らない。

ここまで、簡単のため、球内部の正電荷を一様とし、正面衝突だけを考えてきたが、分布が一様でなく正面衝突でないときも、アルファ粒子が原子によってどのように散乱されるかを計算することができる。それによれば、正電荷が小さな領域に閉じ込められていれば、高速のアルファ粒子が跳ね返されることがあり、その割合も計算できるが、正電荷が広がっている場合は、高速のアルファ粒子が大きく跳ね返されることはない。ラザフォードの指導のもと、ガイガーとマーステンは金属箔にアルファ線を照射し、跳ね返り方を調べたが、結果は驚くべきものであった。大きく跳ね返されるアルファ粒子があり、定量的に調べると、原子の正電荷は原子全体の半径の10000分の1以下の半径の領域に集中しているとすると実験結果とよく合うことが分かったのである。このようにして$\fbox{45}$が発見され、ミクロの世界への理解が飛躍的に進展するきっかけとなった。

• 問1
  • (1) 文中の$\fbox{32}$に入る文として最も適切なものを、次の(a)～(c)のうちから1つ選べ。
    • (a) 電子の強い引力を大きく受けるが、引力がない正電荷は影響を受けない
    • (b) 軽い電子にはあまり影響されず、重い正電荷の影響を大きく受ける
    • (c) 電子の引力と正電荷の反発力の双方から同様に大きな形響を受ける
  • (2) 文中の$\fbox{33}$に入る言葉として最も適切なものを、次の(a)～(e)のうちから1つ選べ。
    • (a) 軽い電子
    • (b) アルファ粒子
    • (c) 重い正電荷
    • (d) 軽い負電荷
    • (e) 重い正電荷と軽い負電荷
• 問2
  • (1) 文中の$\fbox{34}$、$\fbox{35}$に入る式として最も適切なものを、次の(a)～(i)のうちからそれぞれ1つずつ選べ。
    • (a) $\dfrac{k_0eQ}{r}$
    • (b) $\dfrac{2k_0eQ}{r}$
    • (c) $\dfrac{3k_0eQ}{r}$
    • (d) $-\dfrac{k_0eQ}{r}$
    • (e) $-\dfrac{2k_0eQ}{r}$
    • (f) $-\dfrac{3k_0eQ}{r}$
    • (g) $\dfrac{k_0eQ}{r^2}$
    • (h) $\dfrac{2k_0eQ}{r^2}$
    • (i) $\dfrac{3k_0eQ}{r^2}$
  • (2) 文中の$\fbox{36}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $\sqrt{\dfrac{E_0}{m}}$
    • (b) $\sqrt{\dfrac{2E_0}{m}}$
    • (c) $\sqrt{\dfrac{3E_0}{m}}$
    • (d) $\sqrt{\dfrac{1}{m}\left(E_0-k_0\dfrac{eQ}{r}\right)}$
    • (e) $\sqrt{\dfrac{2}{m}\left(E_0-k_0\dfrac{eQ}{r}\right)}$
    • (f) $\sqrt{\dfrac{3}{m}\left(E_0-k_0\dfrac{eQ}{r}\right)}$
    • (g) $\sqrt{\dfrac{1}{m}\left(E_0-k_0\dfrac{2eQ}{r}\right)}$
    • (h) $\sqrt{\dfrac{2}{m}\left(E_0-k_0\dfrac{2eQ}{r}\right)}$
    • (i) $\sqrt{\dfrac{3}{m}\left(E_0-k_0\dfrac{2eQ}{r}\right)}$
  • (3) 文中の$\fbox{37}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $\dfrac{k_0eQ}{E_0}$
    • (b) $\dfrac{2k_0eQ}{E_0}$
    • (c) $\dfrac{3k_0eQ}{E_0}$
    • (d) $\dfrac{E_0}{k_0eQ}$
    • (e) $\dfrac{2E_0}{k_0eQ}$
    • (f) $\dfrac{3E_0}{k_0eQ}$
    • (g) $\dfrac{2E_0}{k_0eQ}$
    • (h) $\dfrac{3E_0}{k_0eQ}$
    • (i) $\dfrac{3E_0}{2k_0eQ}$
  • (4) 文中の$\fbox{38}$に入る言葉として最も適切なものを、次の(a)～(b)のうちから1つ選べ。
    • (a) 大きい
    • (b) 小さい
• 問3
  • (1) 文中の$\fbox{39}$～$\fbox{42}$に入る式として最も適切なものを、次の(a)～(i)のうちからそれぞれ1つずつ選べ。
    • (a) $\dfrac{k_0eQR}{R}$
    • (b) $\dfrac{2k_0eQR}{R}$
    • (c) $\dfrac{3k_0eQR}{R}$
    • (d) $-\dfrac{k_0eQR}{R}$
    • (e) $-\dfrac{2k_0eQR}{R}$
    • (f) $-\dfrac{3k_0eQR}{R}$
    • (g) $-\dfrac{k_0eQR}{R^3}$
    • (h) $-\dfrac{2k_0eQR}{R^3}$
    • (i) $-\dfrac{3k_0eQR}{R^3}$
  • (2) 文中の$\fbox{43}$に入る式として最も適切なものを、次の(a)～(i)のうちから1つ選べ。
    • (a) $\dfrac{k_0eQR}{E_0}$
    • (b) $\dfrac{2k_0eQR}{E_0}$
    • (c) $\dfrac{3k_0eQR}{E_0}$
    • (d) $\dfrac{E_0}{k_0eQR}$
    • (e) $\dfrac{E_0}{2k_0eQR}$
    • (f) $\dfrac{E_0}{3k_0eQR}$
    • (g) $\dfrac{2E_0}{k_0eQR}$
    • (h) $\dfrac{3E_0}{k_0eQR}$
    • (i) $\dfrac{3E_0}{2k_0eQR}$
  • (3) 文中の$\fbox{44}$に入る言葉として最も適切なものを、次の(a)～(b)のうちから1つ選べ。
    • (a) 大きい
    • (b) 小さい
• 問4 文中の$\fbox{45}$に入る言葉として最も適切なものを、次の(a)～(e)のうちから1つ選べ。
  • (a) 放射能
  • (b) アルファ粒子の散乱
  • (c) 原子内の電子分布
  • (d) 原子核
  • (e) 原子エネルギー