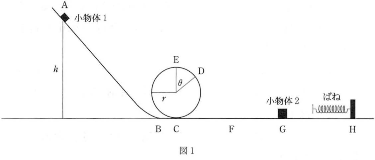
図1のように、高さ$h$の点Aから曲線に沿って点Bを通過し、点Cから半径$r$の鉛直な円形のループを経て、水平部分の点F、G、Hと続くレールがある。なお、点Cはループの最下点であり、点B、C、F、G、Hは同一水平面内にある。点Gには、質量$m_2$の小物体2が置かれ、点Hには、ばね定数$k$、自然長$l$のつるまきばねが固定されている。レール上、質量$m_1$の小物体1が点Aから静かに運動をはじめ、点Cを通過しループへと進んだ。重力加速度の大きさを$g$とし、小物体がレール上を運動するときの摩擦や空気の抵抗、小物体の大きさは無視できるものとする。

• 問1 高さ$h$で小物体1が運動をはじめる前の運動エネルギーは$\fbox{1}$であり、重力による位置エネルギーは$\fbox{2}$である。ただし、重力による位置エネルギーの基準は点B、C、F、G、Hを含む水平面とする。

  $\fbox{1}$、$\fbox{2}$に入る式として最も適切なものを、次の(1)～(9)のうちからそれぞれ1つずつ選べ。

  • (1) 0
  • (2) $m_1gr$
  • (3) $2m_1gr$
  • (4) $m_1gh$
  • (5) $m_1g(h-r)$
  • (6) $m_1g(h-2r)$
  • (7) $m_1g(h+r)$
  • (8) $\dfrac{1}{2}m_1h^2$
  • (9) $\dfrac{1}{2}m_1r^2$
• 問2 点Cでの小物体1の速さは$v_\text{c}=\fbox{3}$となる。$\fbox{3}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
  • (1) 0
  • (2) $\sqrt{2gr}$
  • (3) $2\sqrt{gr}$
  • (4) $\sqrt{2g(h-r)}$
  • (5) $\sqrt{2g(h-2r)}$
  • (6) $\sqrt{2gh}$
  • (7) $2\sqrt{gh}$
  • (8) $\sqrt{2g(h+r)}$
  • (9) $\sqrt{2g(h+2r)}$
• 問3 小物体1が点Cを通過する直前のレールから受ける垂直抗力は、$N_\text{c}=\fbox{4}$である。また小物体1が点Cを通過する直後のレールから受ける垂直抗力は$N_\text{c}'=\fbox{5}$である。$\fbox{4}$、$\fbox{5}$に入る式として最も適切なものを、次の(1)～ (9)のうちからそれぞれ1つずつ選べ。
  • (1) 0
  • (2) $m_1g$
  • (3) $m_1g\bigg(1+\dfrac{h}{r}\bigg)$
  • (4) $m_1g\bigg(1+\dfrac{h}{2r}\bigg)$
  • (5) $m_1g\bigg(1+\dfrac{2h}{r}\bigg)$
  • (6) $m_1g\bigg(1-\dfrac{h}{r}\bigg)$
  • (7) $m_1g\bigg(1-\dfrac{h}{2r}\bigg)$
  • (8) $m_1g\bigg(1-\dfrac{2h}{r}\bigg)$
  • (9) $m_1g(h+r)$
• 問4 点Dで小物体1がレールから受ける垂直抗力$N_\text{D}$を考える。ただし、ループの点Cの真上の点E(ループの最高点)と点Dの中心角を$\theta$とする。次の(1)～(3)に答えよ。

  • (1) 点Dにおいて、小物体1は鉛直下方への重力$\fbox{6}$、レールからの垂直抗力$N_\text{D}$、遠心力$F_\text{D}=\fbox{7}$を受けて運動する。ただし、点Dにおける小物体1の速さを$v_\text{D}$とする。

    $\fbox{6}$、$\fbox{7}$に入る式として最も適切なものを、次の(1)～(9)のうちからそれぞれ1つずつ選べ。

    • (1) $m_1g$
    • (2) $m_1g\sin\theta$
    • (3) $m_1g\cos\theta$
    • (4) $\dfrac{1}{2}m_1{v_\text{D}}^2$
    • (5) $m_1{v_\text{D}}^2$
    • (6) $m_1\dfrac{v_\text{D}}{r}$
    • (7) $m_1\dfrac{{v_\text{D}}^2}{r}$
    • (8) $\dfrac{1}{2}m_1v_\text{D}$
    • (9) $\dfrac{1}{2}m_1\dfrac{{v_\text{D}}^2}{r}$
  • (2) 小物体1のレールと垂直方向の力のつりあいの式は$0=\fbox{8}$となる。$\fbox{8}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
    • (1) $N_\text{D}+m_1g\sin\theta+F_\text{D}$
    • (2) $N_\text{D}+m_1g\sin\theta-F_\text{D}$
    • (3) $N_\text{D}+m_1g\cos\theta+F_\text{D}$
    • (4) $N_\text{D}+m_1g\cos\theta-F_\text{D}$
    • (5) $N_\text{D}-m_1g\sin\theta+F_\text{D}$
    • (6) $N_\text{D}-m_1g\sin\theta-F_\text{D}$
    • (7) $N_\text{D}-m_1g\cos\theta+F_\text{D}$
    • (8) $N_\text{D}-m_1g\cos\theta-F_\text{D}$
    • (9) $N_\text{D}-m_1g\sin\cos\theta=F_\text{D}$
  • (3) 力学的エネルギー保存の式から$v_\text{D}=\fbox{9}$となり、これから、$N_\text{D}=m_1g\times(\fbox{10}) となる。$\fbox{9}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
    • (1) $\sqrt{2gr(1+\sin\theta)}$
    • (2) $\sqrt{2gr(1+\cos\theta)}$
    • (3) $\sqrt{2ghr(1+\sin\theta)}$
    • (4) $\sqrt{2ghr(1+\cos\theta)}$
    • (5) $\sqrt{2g\{h+r(1+\sin\theta)\}}$
    • (6) $\sqrt{2g\{h+r(1+\cos\theta)\}}$
    • (7) $\sqrt{2g\{h-r(1+\sin\theta)\}}$
    • (8) $\sqrt{2g\{h-r(1+\cos\theta)\}}$
    • (9) $\sqrt{2g\{h-r(1-\sin\theta)\}}$
    また、$\fbox{10}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
    • (1) $\dfrac{2h}{r}-\sin\theta-\cos\theta$
    • (2) $\dfrac{2h}{r}-1-\sin\theta$
    • (3) $\dfrac{2h}{r}-1-\cos\theta$
    • (4) $\dfrac{2h}{r}-1-2\sin\theta$
    • (5) $\dfrac{2h}{r}-1-2\cos\theta$
    • (6) $\dfrac{2h}{r}-1-3\sin\theta$
    • (7) $\dfrac{2h}{r}-1-3\cos\theta$
    • (8) $\dfrac{2h}{r}-2-3\sin\theta$
    • (9) $\dfrac{2h}{r}-2-3\cos\theta$

• 問5 小物体1が点Eでレールから離れないで通過するためには、はじめの高さは$h\geqq h_1=\fbox{11}$でなければならない。

  $\fbox{11}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。

  • (1) $r$
  • (2) $\dfrac{3}{2}r$
  • (3) $2r$
  • (4) $\dfrac{5}{2}r$
  • (5) $3r$
  • (6) $\dfrac{7}{2}r$
  • (7) $4r$
  • (8) $\dfrac{9}{2}r$
  • (9) $5r$
• 問6 つぎに、小物体1を$h_1$より高い位置$h$から静かに手を離した。小物体1はループを通過し、点Gで質量$m_2$の小物体2に完全非弾性衝突し、衝突後は小物体1と小物体2は一体(以下「小物体12」と呼ぶ)となって運動した。衝突後の小物体12の速さは$V=\fbox{12}$である。$\fbox{12}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
  • (1) $(m_1+m_2)\sqrt{2gh}$
  • (2) $\dfrac{1}{m_1+m_2}\sqrt{2gh}$
  • (3) $\dfrac{m_1}{m_1+m_2}\sqrt{2gh}$
  • (4) $\dfrac{m_1+m_2}{m_1}\sqrt{2gh}$
  • (5) $\dfrac{m_1m_2}{m_1+m_2}\sqrt{2gh}$
  • (6) $\dfrac{m_1+m_2}{m_1m_2}\sqrt{2gh}$
  • (7) $\dfrac{m_1+m_2}{m_2}\sqrt{2gh}$
  • (8) $\dfrac{m_2}{m_1+m_2}\sqrt{2gh}$
  • (9) $\dfrac{m_1}{m_2}\sqrt{2gh}$
• 問7 この小物体1と小物体2の衝突で、失われた力学的エネルギーは$\Delta E=\fbox{13}$である。$\fbox{13}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
  • (1) $(m_1+m_2)gh$
  • (2) $\dfrac{{m_1}^2}{m_1+m_2}gh$
  • (3) $\dfrac{{m_2}^2}{m_1+m_2}gh$
  • (4) $\dfrac{2{m_1}^2}{m_1+m_2}gh$
  • (5) $\dfrac{2{m_2}^2}{m_1+m_2}gh$
  • (6) $\dfrac{m_1m_2}{m_1+m_2}gh$
  • (7) $\dfrac{2m_1m_2}{m_1+m_2}gh$
  • (8) $\dfrac{{m_1}^2}{2(m_1+m_2)}gh$
  • (9) $\dfrac{{m_2}^2}{2(m_1+m_2)}gh$
• 問8 衝突後一体となった小物体12は、前方のばねを押し縮め、その後逆方向に運動した。このとき、力学的エネルギーは保存されるものとすると、このときのばねの縮みの最大値は$x_0=\fbox{14}$となる。$\fbox{14}$に入る式として最も適切なものを、次の(1)～(9)のうちから1つ選べ。
  • (1) $\sqrt{\dfrac{2m_1gh}{k}}$
  • (2) $\sqrt{\dfrac{{m_1}^2gh}{km_2}}$
  • (3) $\sqrt{\dfrac{2{m_2}^2gh}{km_1}}$
  • (4) $\sqrt{\dfrac{m_1m_2gh}{k(m_1+m_2)}}$
  • (5) $\sqrt{\dfrac{{m_1}^2gh}{k(m_1+m_2)}}$
  • (6) $\sqrt{\dfrac{{m_2}^2gh}{k(m_1+m_2)}}$
  • (7) $\sqrt{\dfrac{2m_1m_2gh}{k(m_1+m_2)}}$
  • (8) $\sqrt{\dfrac{2{m_1}^2gh}{k(m_1+m_2)}}$
  • (9)$\sqrt{\dfrac{2{m_2}^2gh}{k(m_1+m_2)}}$