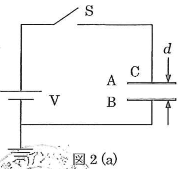
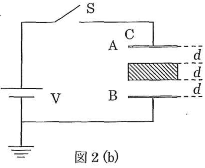
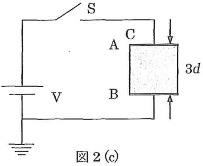
図2(a)に示される回路において、電池$\text{V}$の起電力を$V$[V]、間隔$d$[m]の極板$\text{A}$、$\text{B}$からなる平行板コンデンサー$\text{C}$の静電容量を$C$[F]とする。まずスイッチ$\text{S}$を閉じて電流を流し、十分時間がたってから$\text{S}$を開いた。以後$\text{S}$は開いた状態とし、接地面の電位を$0$Vとする。また、$\text{A}$、$\text{B}$の面積は十分大きく、$\text{AB}$間につくられる電場(電界)は一様であり、空気中の比誘電率を1とする。このとき$\text{AB}$間の電場(電界)の大きさは(1)「V/m]、静電エネルギーは(2)[J]であり、$\text{A}$にたまる電気量(電荷)は(3)[C]である。

$\text{A}$と$\text{B}$との間隔を$d$[m]から$3d$[m]にした。このとき$\text{C}$の静電容量は(4)[F]であり、$\text{AB}$間の電場(電界)の大きさは(5)[V/m]、静電エネルギーは(6)[J]、$\text{A}$の電位は(7)[V]である。

次に図2(b)に示されるように、$3d$[m]の極板間隔のまま、電気量(電荷)の蓄えられていない絶縁された厚さ$d$[m]の導体板を$\text{AB}$間の中央に、両極板に触れないように挿入した。このとき$\text{C}$の静電容量は(8)[F]、$\text{A}$と導体間との電場(電界)の大きさは(9)[V/m]、$\text{AB}$間の静電エネルギーは(10)[J]、$\text{A}$の電位は(11)[V]である。

導体板を抜き、図2(c)に示されるように比誘電率$\epsilon_r$の誘電体を$\text{AB}$間にすきまなく挿入した。このとき$\text{C}$の静電容量は(12)[F]、誘電体中の電界(電場)の大きさは(13)[V/m]、$\text{AB}$間の静電エネルギーは(14)[J]、$\text{A}$の電位は(15)[V]である。