東邦大学数学2013年第1問
- $\fbox{1}$$x^9-1$を$x+1$で割ったときの商を$P(x)$とするとき、$P(x)$を$x-2$で割ったときの余りは$\fbox{アイウ}$である。
- $\fbox{2}$$x$を実数とする。$104$、$5x$、$x^2$が三角形の3辺の長さとなるような$x$の値の範囲は$\fbox{エ}\lt x\lt\fbox{オカ}$である。
- $\fbox{3}$$0^\circ\leqq\theta\leqq 90^\circ$の$\theta$に対して、$7\sin\theta+\cos\theta=5$が成り立っているとき、$\dfrac{\sin\theta}{1+\cos\theta}+\dfrac{\cos\theta}{1+\sin\theta}$の値は$\dfrac{\fbox{キ}}{\fbox{ク}}$である。
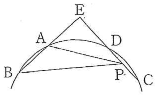
- $\fbox{4}$右図のように、円周上の4点$\text{A}$、$\text{B}$、$\text{C}$、$\text{D}$に対して、直線$\text{AB}$と直線$\text{CD}$の交点を$\text{E}$とし、$\text{AB}=4$、$\text{AE}=5$、$\angle{\text{AED}}=90^\circ$とする。線分$\text{CD}$上を動く点$\text{P}$が$\angle{\text{AFP}}$を最大にするとき、$\text{EP}=\fbox{ケ}\sqrt{\fbox{コ}}$である。
- $\fbox{5}$座標平面上に、原点$(0,~0)$から出発する動点$\text{P}$がある。サイコロを1回ふり、1または2の目が出たとき点$\text{P}$は$x$軸の正の方向に1だけ移動し、3または4の目が出たときは$y$軸の正の方向に1だけ移動し、5または6の目が出たときは動かないとする。
サイコロを4回ふった結果、点$\text{P}$が原点$(0,~0)$から点$(m,~n)$に移動する確率を$\text{P}(m,~n)$で表すとき、$\sum\limits_{k=0}^2\text{P}(2,~k)=\dfrac{\fbox{サ}}{\fbox{シス}}$である。 - $\fbox{6}$数列$\dfrac{1}{2},~\dfrac{3}{4},~\dfrac{3}{2},~\dfrac{5}{6},~\dfrac{5}{4},~\dfrac{5}{2},~\dfrac{7}{8},~\dfrac{7}{6},~\dfrac{7}{4},~\dfrac{7}{2},~\dfrac{9}{10},~\dfrac{9}{8},~\cdots$において、第250項は$\dfrac{\fbox{セソ}}{\fbox{タ}}$である。
- $\fbox{7}$$(1-x)^5(1+y)^6\left(1-\dfrac{1}{x}+\dfrac{1}{y}\right)^7$の展開式における、$x^4y^5$の項の係数は、$\fbox{チツテ}$である。
- $\fbox{8}$実数$x$、$y$、$z$が、$\log_4z=-\dfrac{1}{2}+\log_2\sqrt{\dfrac{x+y}{2}}$、$27^{xy-1}=3^{z+2xy+2}$を満たすとき、$z$の取りうる値の範囲は$z\geqq\dfrac{\fbox{ト}}{\fbox{ナ}}$である。
- $\fbox{9}$$x$を自然数とし、$e$を自然対数の底とする。$n$の関数$f(n)$を、$f(n)=\log_e(_{2n}C_n)+n\left\{1-\log_e\left(\dfrac{n}{4!}\right)\right\}+\log_e(n!)$で定める。
$X=\lim\limits_{n\to\infty}\dfrac{f(n)}{n}$とおくとき、$e^X=\fbox{ニヌ}$である。 - $\fbox{10}$関数$f(x)=\sqrt{2+x}$について、$\lim\limits_{h\to\infty}{\dfrac{1}{h}\left\{\dfrac{f(2+h)}{f(2-h)}-\left(\dfrac{3-h}{3+h}\right)^3\right\}}=\dfrac{\fbox{ネ}}{\fbox{ノ}}$である。
- $\fbox{11}$実数$x$、$y$が、$x^2+y^2\leqq\dfrac{3}{2}$を満たすとき、$\dfrac{y}{{x-2}^2}$の最大値は$\dfrac{\sqrt{\fbox{ハ}}}{\fbox{ヒ}}$である。
- $\fbox{12}$$a$、$b$、$c$、$d$を正の実数とし、$ad-bc\neq 0$とする。行列$A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$について、$A-A^{-1}=\left(\begin{array}{cc}-3&6\\6&3\end{array}\right)$が成り立つとき、$a+d=\fbox{フ}$、$ad-bc=\fbox{ヘ}$である。
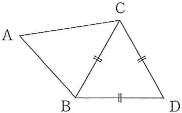
- $\fbox{13}$三角形$\text{ABC}$は、3辺の長さがそれぞれ$\text{AB}=3$、$\text{BC}=\sqrt{13}$、$\text{CA}=4$である。辺$\text{BC}$を共有する正三角形$\text{CBD}$が三角形$\text{ABC}$の外側にあるとき、$\overrightarrow{\text{AD}}=\dfrac{\fbox{ホ}}{\fbox{マ}}\overrightarrow{\text{AB}}+\dfrac{\fbox{ミ}}{\fbox{ム}}\overrightarrow{\text{AC}}$である。
- $\fbox{14}$関数$f(x)$が、等式$f(x)=x^2-4-\dfrac{1}{4}\displaystyle\int_{-2}^2(x-2)|f(t)|dt$を満たすとき、$f\left(-\dfrac{1}{2}\right)$の値は$\dfrac{\fbox{メ}}{\fbox{モ}}$である。
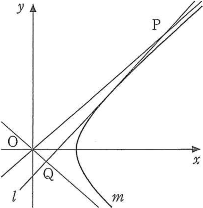
- $\fbox{15}$$\text{O}$を原点とする座標平面上に、双曲線$m:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(b\gt a\gt 0)$があり、$m$上のある点における接線$l$は$x$軸と点$(\sqrt{2},~0)$で交わる。$l$と、$m$、の2つの漸近線との交点のうち、$x$座標の大きいほうを$\text{P}$、小さいほうを$\text{Q}$とする。三角形$\text{OPQ}$の面積が$3\sqrt{6}$、$\text{OP}\cdot\text{OQ}=15$のとき、$\text{PQ}=\fbox{ヤ}\sqrt{\fbox{ユヨ}}$である。