東邦大学数学2012年第1問

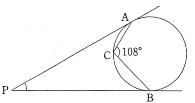
$\fbox{1}$ 右図のように、円周上に3点$\text{A}$、$\text{B}$、$\text{C}$があり、$\angle\text{ACB}=108^\circ$である。円の外部にある点$\text{P}$から円に引いた2つの接線が$\text{A}$と$\text{B}$で接するとき、$\angle\text{APB}=\fbox{アイ}^\circ$である。
$\fbox{2}$ 1から1000までの自然数のうち、3の倍数全体の集合を$A$、5の倍数全体の集合を$B$、7の倍数全体の集合を$C$で表す。このとき、集合$(A\cup B)\cap C$の要素の個数は$\fbox{ウエ}$である。
$\fbox{3}$ $a$、$b$、$c$、$d$をそれぞれ定数とし、座標平面上で行列$\begin{pmatrix} a & b \\ c & d \end{pmatrix}$の表す1次変換を$f$とする。$f$によって、2点$(1, 1)$、$(1, -1)$がそれぞれ$(12, 7)$、$(8, -9)$に移るとき、$a+d$の値は$\fbox{オカ}$である。
$\fbox{4}$ 3個のサイコロを同時にふるとき、出た目のうち最大の目が4かつ最小の目が3となる確率は$\dfrac{\fbox{キ}}{\fbox{クケ}}$である。
$\fbox{5}$ 極限$\displaystyle\lim_{x\to0}\dfrac{1}{x}\bigg(\dfrac{1}{\sqrt{3-\sin x}}-\dfrac{1}{\sqrt{3+\sin x}}\bigg)$の値は$\dfrac{\sqrt{\fbox{コ}}}{\fbox{サ}}$である。
$\fbox{6}$ $k$を定数とする。2つの2次方程式 \[2x^2+kx-1=0\]\[2x^2-2x+k+1=0\] が共通の解をただ一つもつとき、$k$の値は$\fbox{シス}$である。
$\fbox{7}$ 2つの実数$x$、$y$が$\dfrac{1}{8^x}=\dfrac{1}{27^y}=36$を満たすとき、
$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{\fbox{セソ}}{\fbox{タ}}$である。
$\fbox{8}$ $a$を定数とする。座標平面上の2つの曲線$y=a(x^2+1)$と$y=2x^2-x^3$が相違なる3つの点で交わるとき、$a$の取りうる値の範囲は
$\fbox{チ}\lt a\lt\dfrac{\fbox{ツ}}{\fbox{テ}}$である。
$\fbox{9}$ 空間において、2点$(0,0,0)$、$(1,1,1)$を通る直線を$l$、2点$(1,0,0)$、$(0,1,0)$を通る直線を$m$とする。
$l$上の点と$m$上の点の間の距離の最小値は$\dfrac{\sqrt{\fbox{ト}}}{\fbox{ナ}}$である。
$\fbox{10}$ $a$、$b$、$c$、$d$をそれぞれ定数とする。座標平面上の曲線$y=x^4+ax^3+bx^2+cx+d$は、$x=0$で$x$軸に接し、かつ異なる2つの点で直線$y=x-9$に接するとする。このとき、$a$の値は$\dfrac{\fbox{ニ}}{\fbox{ヌ}}$である。
$\fbox{11}$ 3次方程式$x^3-x^2-4x-1=0$の3つの解を$\alpha$、$\beta$、$\gamma$とするとき、$\bigg(\alpha+\dfrac{1}{\alpha}\bigg)\bigg(\beta+\dfrac{1}{\beta}\bigg)\bigg(\gamma+\dfrac{1}{\gamma}\bigg)=\fbox{ネノ}$である。
$\fbox{12}$ $0\leqq t\leqq\sqrt{2}$を定義域とする$t$の関数$\displaystyle\int_0^\frac{3}{2}\Bigg|t-\sqrt{2-\dfrac{4}{3}x}\Bigg|dx$の最小値は$\fbox{ハヒ}+\sqrt{\fbox{フ}}$である。
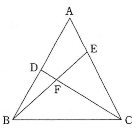
$\fbox{13}$ $\triangle\text{ABC}$において、$\text{AB}=\text{CA}=13$、$\text{BC}=10$とする。また、辺$\text{AB}$の中点を$\text{D}$、辺$\text{CA}$を$2:1$に内分する点を$\text{E}$、線分$\text{CD}$と線分$\text{BE}$の交点を$\text{F}$とする。このとき、$\triangle\text{CEF}$の面積は$\fbox{ヘホ}$である。
$\fbox{14}$ 座標平面において、3直線$y=0$、$4x+3y-4=0$、$12x-5y=0$に囲まれてできる三角形の内心の$x$座標は、$\dfrac{\fbox{マ}}{\fbox{ミ}}$である。
$\fbox{15}$ 実数$x$に対して$n\leqq x\lt n＋1$を満たす整数$n$を$[~x~]$で表すとき、
$\displaystyle\sum_{k=1}^{50}\bigg[\dfrac{3}{5}k\bigg]$の値は$\fbox{ムメモ}$である。