東京女子医科大学物理2012年第2問
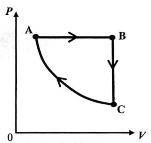
気体は仕事および熱を周囲と相互に$\dot{や}\dot{り}\dot{と}\dot{り}$することでその状態を変化させる。図に示す圧力$P$と体積$V$のグラフは、1モル理想気体が状態Aから3つの過程を右回りに一巡して状態Aに戻る状態変化を表す。A→B過程は定圧変化、B→C過程は定積変化、さらにC→A過程は断熱変化である。これらの過程における仕事および熱の$\dot{や}\dot{り}\dot{と}\dot{り}$を考えよう。
状態A、BおよびCの気体温度を$T_\text{A}$、$T_\text{B}$および$T_\text{C}$で、圧力を$P_\text{A}$、$P_\text{B}$および$P_\text{C}$で、体積を$V_\text{A}$、$V_\text{B}$および$V_\text{C}$で、それぞれ表す。気体定数を$R$で、この気体の定積モル比熱を$C_\text{V}$で表す。

- (1) 以下のア)~ウ)の過程に当てはまる記述を下欄に示すa~fから二つずつ選んでそれらの記号を選択欄に記し、ア)~エ)の文中の(1)~(17)には適切な文字式を入れよ。
選択肢- a. 気体が周囲に仕事をする。
- b. 気体が周囲から仕事をされる。
- c. 周囲との仕事の$\dot{や}\dot{り}\dot{と}\dot{り}$はない。
- d. 気体が周囲に熱を与える。
- e. 気体が周囲から熱を受ける。
- f . 周囲との熱の$\dot{や}\dot{り}\dot{と}\dot{り}$はない。
- ア) A→B過程
この過程は定圧変化であるからシャルルの法則 $\fbox{1}=\fbox{2}$が成り立ち、気体温度について$\fbox{3}\gt\fbox{4}$である。この過程で気体が周囲と$\dot{や}\dot{り}\dot{と}\dot{り}$する仕事の大きさは$P_\text{A}\big(\fbox{5}\big)$に等しく、熱量の大きさは、$P_\text{A}\big(\fbox{5}\big)$と$C_\text{V}\big(\fbox{6}\big)$の和に等しい。
- イ) B→C過程
この過程は定積変化であるから、気体温度について$\fbox{7}\gt\fbox{8}$である。この過程で気体が周囲と$\dot{や}\dot{り}\dot{と}\dot{り}$する熱量の大きさは$C_\text{V}\big(\fbox{9}\big)$に等しい。
- ウ) C→A過程
この過程は断熱変化であるから気体が周囲と$\dot{や}\dot{り}\dot{と}\dot{り}$する仕事の大きさは$C_\text{v}\big(\fbox{10}\big)$に等しい。このことから、気体温度について$\fbox{11}\gt\fbox{12}$である。
- エ) 結局、$T_\text{A}$、$T_\text{B}$および$T_\text{C}$の間には$\fbox{13}\gt\fbox{14}\gt\fbox{15}$の大小関係がある。また、A→B→C→Aと状態を一巡する間に気体が周囲から受けた熱量の大きさは$R\big(\fbox{16}\big)+C_\text{V}\big(\fbox{17}\big)$である。
- (2) A→B→C→Aと状態を一巡する間に気体が周囲から受けた熱量は、図のグラフで囲まれた部分の面積で表される。その理由を述べよ。