愛知医科大学数学2012年第3問
$\text{AB}=4$、$\text{AC}=3$、$\angle{\text{A}}=\dfrac{\pi}{2}$の三角形$\text{ABC}$に対して、3直線$l_1$、$l_2$、$l_3$は以下の条件を満たす。
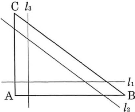 $l_1$と直線$\text{AB}$ではさまれる領域を$\text{P}$、$l_2$と直線$\text{BC}$ではさまれる領域を$\text{Q}$、$l_3$と直線$\text{CA}$ではさまれる領域を$\text{R}$とする。条件iii)で与えられた距離を$x$とするとき、和集合$\text{P}{\cup}\text{Q}{\cup}\text{R}$と三角形$\text{ABC}$の共通部分の面積$S(x)$を求め、そのグラフをかけ。
$l_1$と直線$\text{AB}$ではさまれる領域を$\text{P}$、$l_2$と直線$\text{BC}$ではさまれる領域を$\text{Q}$、$l_3$と直線$\text{CA}$ではさまれる領域を$\text{R}$とする。条件iii)で与えられた距離を$x$とするとき、和集合$\text{P}{\cup}\text{Q}{\cup}\text{R}$と三角形$\text{ABC}$の共通部分の面積$S(x)$を求め、そのグラフをかけ。
- i) $l_1$、$l_2$、$l_3$はいずれも三角形$\text{ABC}$の内部を通る。
- ii) $l_1$と$\text{AB}$、$l_2$と$\text{BC}$、$l_3$と$\text{CA}$はそれぞれ平行である。
- iii) $l_1$と$\text{AB}$、$l_2$と$\text{BC}$、$l_3$と$\text{CA}$の間の距離は全て等しい。
