愛知医科大学物理2012年第2問

問1.となり合うスリットの間隔がdの薄い回折格子シートがある。図1のように、波長λの平行光線を回折格子シートに対して垂直に入射させると、それぞれのスリットから出る光は特定の方向で強め合い、遠くにあるスクリーン上に干渉縞を生じる。このとき直進する光を除いて、入射光の方向に対して最も小さい角度で強め合う光を1次回折光という。ここでとなり合うスリットから出る1次回折光の角度はθ1であった。
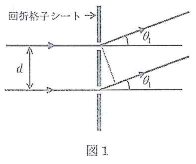
1. となり合うスリットを通る1次回折光の経路差を、 $d$ 、 $\theta_1$ を用いて表せ。
2. $\sin\theta_1$ を、 $d$ 、 $i$ 、 $\lambda$ を用いて表せ。
問2.次に、図2のように、波長λの平行光線を回折格子シートに対して入射角iで入射させたところ、1次回折光の角度が大きくなった。このときの回折角θ2であった。
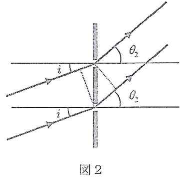
1. となり合うスリットを通る1次回折光の経路差を、 $d$ 、 $i$ 、 $\theta_2$ を用いて表せ。
2. $\sin\theta_2$ を、 $d$ 、 $i$ 、 $\lambda$ を用いて表せ。
問3.図3のように、屈折率nの両面が平行なガラス板の右側に、となり合うスリットの間隔がdの薄い回折格子シートを取り付けた。そして波長λの平行光線をガラス面に対して入射角iで入射させたところ、屈折角rで屈折してガラス内を通過し、回折格子によって1次回折光は角度θ3で回折した。空気の屈折率を1とし、ガラス板の厚さは、スリットの間隔に比べて十分に厚いものとする。
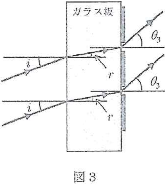
1. ガラス内での光の波長を、 $n$ 、 $\lambda$ を用いて表せ。
2. $\sin{i}$ を、 $n$ 、 $r$ を用いて表せ。
3. 屈折率 $n$ のガラス内を光が距離 $L$ 進む時間に、屈折率が $1$ の空間を光が進む距離(光学距離)を、 $n$ 、 $L$ 、 $\lambda$ の中から必要なものを用いて表せ。
4. となり合うスリットを通る光の、回折格子の両側での1次回折光の光学距離の差を、 $d$ 、 $n$ 、 $r$ 、 $\theta_3$ を用いて表せ。
5. $\theta_3$ を、 $d$ 、 $I$ 、 $n$ 、 $\lambda$ の中から必要なものを用いて表せ。
問4.次に、図4のように、回折格子シートを取り外してガラス板の左側に取り付けた。そして波長λの平行光線を回折格子シートに対してある入射角i0で入射させたところ、1次回折光はガラス内を直進した後、ガラス面の右側で屈折角θ4で屈折した。
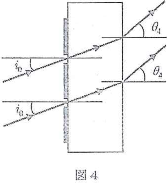
1. となり合うスリットを通る光の回折格子の両側での1次回折光の光学距離の差を、 $d$ 、 $i_0$ 、 $n$ を用いて表せ。
2. $\sin{i_0}$ を、 $d$ 、 $n$ 、 $\lambda$ を用いて表せ。
3. $\sin\theta_4$ を、 $d$ 、 $i_0$ 、 $\lambda$ を用いて表せ。