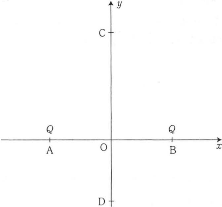
図のように、真空中に直交する$xy$座標軸をとり、原点$\text{O}$からそれぞれ距離$a$〔m〕の点$\text{A}(-a,~0)$と点$\text{B}(a,~0)$にそれぞれ、電気量$Q$〔C〕の正の点電荷を固定する。クーロンの法則の比例定数を$k_0$〔N・m²/C²〕とし、無限遠点での電位を0とする。

• 問1 点$\text{C}(0,~\sqrt{3}a)$における電場(電界)の強さは何N/Cか、また電場の向きはどの向きか。これらの組合せとして正しいものを、次の(1)～(6)から一つ選びなさい。$\fbox{1}$
  • (1) $\dfrac{\sqrt{2}k_0Q}{4a^2}$、$y$軸負の向き
  • (2) $\dfrac{\sqrt{3}k_0Q}{4a^2}$、$y$軸負の向き
  • (3) $\dfrac{k_0Q}{2a^2}$、$y$軸負の向き
  • (4) $\dfrac{\sqrt{2}k_0Q}{4a^2}$、$y$軸正の向き
  • (5) $\dfrac{\sqrt{3}k_0Q}{4a^2}$、$y$軸正の向き
  • (6) $\dfrac{k_0Q}{2a^2}$、$y$軸正の向き
• 問2 点$\text{C}(0,~\sqrt{3}a)$の電位は何Vか。正しいものを、次の(1)～(6)から一つ選びなさい。$\fbox{2}$〔V〕
  • (1) $0$
  • (2) $\dfrac{k_0Q}{2a}$
  • (3) $\dfrac{k_0Q}{\sqrt{3}a}$
  • (4) $\dfrac{k_0Q}{a}$
  • (5) $\dfrac{2k_0Q}{\sqrt{3}a}$
  • (6) $\dfrac{2k_0Q}{a}$
• 問3 原点$\text{O}$から$y$軸上で負の向きに十分離れた点において、質量$m$〔kg〕、電気量$q$〔C〕の正の点電荷に、$y$軸正の向きの初速を与えて点$\text{C}$に到達させたい。点電荷に与える初速は何m/sより大きくなくてはならないか。正しいものを、次の(1)～(8)から一つ選びなさい。$\fbox{3}$〔m/s〕
  • (1) $\dfrac{1}{2}\sqrt{\dfrac{k_0Qq}{ma}}$
  • (2) $\sqrt{\dfrac{k_0Qq}{2ma}}$
  • (3) $\sqrt{\dfrac{k_0Qq}{ma}}$
  • (4) $\sqrt{\dfrac{2k_0Qq}{ma}}$
  • (5) $2\sqrt{\dfrac{k_0Qq}{ma}}$
  • (6) $\dfrac{1}{2a}\sqrt{\dfrac{k_0Qq}{m}}$
  • (7) $\dfrac{1}{a}\sqrt{\dfrac{k_0Qq}{m}}$
  • (8) $\dfrac{2}{a}\sqrt{\dfrac{k_0Qq}{m}}$
• 問4 次に、点$\text{D}(0,~-a)$に電気量$-Q$〔C〕の負の点電荷を置いた。その後、点$\text{A}$にある正の点電荷と点$\text{D}$に置いた負の点電荷を置き替えた。この置き替えに必要な仕事は何$\text{J}$か。正しいものを、次の(1)～(6)から一つ選びなさい。$\fbox{4}$〔$\text{J}$〕
  • (1) $(\sqrt{2}-1)\dfrac{k_0Q^2}{a}$
  • (2) $\dfrac{k_0Q^2}{2a}$
  • (3) $\dfrac{k_0Q^2}{a}$
  • (4) $\dfrac{\sqrt{2}k_0Q^2}{a}$
  • (5) $\dfrac{2k_0Q^2}{a}$
  • (6) $(\sqrt{2}+1)\dfrac{k_0Q^2}{a}$