鉛直上向きの一様な磁場（磁束密度$B$）の中に、単位長さあたりの電気抵抗が$\rho$の導線を折り曲げて、図1のABCDEFのような形状を作り、面BCDEが水平になるように置いた。長さ$2L$のBCとDEは、間隔$L$で平行になっており、CDは両辺と垂直である。長さ$3L$のABとEFは、間隔$L$で平行になっており、水平面から角度$\theta$だけ傾いている。導体棒（質量$m$、単位長さあたりの電気抵抗$\rho$）は、導線CBAとDEFの上をCDと常に平行なまま滑ることができる。導体棒と導線CBA、DEFとの接点をそれぞれP、Qとする。導線と導体棒の間の摩擦・空気抵抗・回路のインダクタンスは無視できるものとして、以下の問に答えよ。ただし重力加速度を$g$とする。
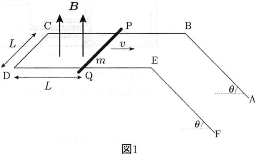
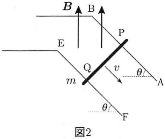
DQの距離が$L$になるように導体棒を置き、時刻0以降は導体棒が一定の速さ$v(\neq0)$でCDから遠ざかる方向へ滑るよう、水平かつ導体棒に垂直な外力を与える（図1）。

• 問1 導体棒を流れる電流の向きは、P→Q・Q→Pのどちらか?
• 問2 時刻$t({\lt}L/v)$で、外力の向きは導体棒をCDに近づける方向・CDから速ざける方向のどちらか?
• 問3 時刻$t({\lt}L/v)$で、閉回路の電気抵抗を求めよ。
• 問4 時刻$t({\lt}L/v)$で、導体棒を流れる電流の大きさを求めよ。
• 問5 時刻$t({\lt}L/v)$で、導体棒に与える外力の大きさを求めよ。

時刻$L/v$以後は、導体棒が一定の速さ$v$で斜面に沿って滑り下るよう、斜面に平行かつ導体棒に垂直に外力を与える（図2）。導体棒はBEをなめらかに通過することができるとする。

• 問6 時刻$t({\lt}L/v)$で、導体棒を流れる電流の大きさを求めよ。
• 問7 $t=2L/v$のとき、導体棒に与える外力の大きさがゼロになった。$B$、$L$、$\rho$、$m$、$g$、$\theta$の中から必要な記号を用いて、$v$の値を表せ。
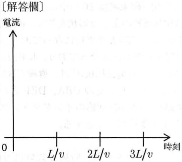
• 問8 時刻$0$～$3L/v$で、導体棒を流れる電流の大きさが変化する様子をグラフに描け。その際に、軸との交点などの特徴的な値も明記すること。