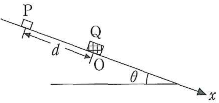
図のように、傾斜角$\theta$の斜面上に、質量$m$の小物体$\text{P}$と質量$2m$の小物体$\text{Q}$を置く。$\text{P}$と斜面の間の摩擦は無視できるが、$\text{Q}$と斜面の間の摩擦は無視できず、動摩擦係数は$\mu$である。$\text{P}$と$\text{Q}$の衝突はじゅうぶんに短い時間に起こり、そのときの摩擦力や重力の影響は無視できるものとする。また、斜面はじゅうぶんに長く、$\text{P}$と$\text{Q}$が斜面の外に出ることはないものとする。はじめ、$\text{Q}$は静止しており、その位置を原点$\text{O}$として斜面に沿って下向きに$x$軸をとる。重力加速度の大きさを$g$として、以下の文中の四角内に入れるのに適当なものを対応する解答群の中からひとつ選び、その番号を解答欄に記入せよ。

$\text{P}$を$x=-d$の位置から静かにはなしたところ、$\text{P}$は斜面をすべり降り、$\text{P}$と$\text{Q}$は弾性衝突して、$\text{Q}$は動き始めた。この衝突の時刻を$t=0$とする。$t=0$で$\text{Q}$と衝突する直前の$\text{P}$の速度は$\fbox{1}$となる。この速度を$v_p$とすると、この衝突直後の$\text{P}$の速度は$\fbox{2}$、$\text{Q}$の速度は$\fbox{3}$となる。この衝突後に動き出した$\text{Q}$の加速度は$\fbox{4}$だから、$\text{Q}$が減速するために$\mu$が満たす必要がある条件を、$\theta$を用いて表すと$\fbox{5}$となる。

$t=0$での衝突の後、$\text{Q}$が静止する前に$\text{P}$と$\text{Q}$が再び衝突した。$t=0$で衝突してから再び衝突するまでのあいだの時刻$t$において、$\text{P}$の加速度は$\fbox{6}$、$\text{P}$の速度は$\fbox{7}$、$\text{P}$の$x$座標は$\fbox{8}$である。また、$\text{Q}$の速度は$\fbox{9}$、$\text{Q}$の$x$座標は$\fbox{10}$である。したがって、再び衝突する時刻は$\fbox{11}$となる。

• (1)
  • [1] $0$
  • [2] $\dfrac{1}{3}\sqrt{2gd\sin\theta}$
  • [3] $\dfrac{2}{3}\sqrt{2gd\sin\theta}$
  • [4] $\sqrt{2gd\sin\theta}$
• (2)
  • [1] $-\dfrac{1}{3}v_p$
  • [2] $0$
  • [3] $\dfrac{1}{3}v_p$
  • [4] $\dfrac{2}{3}v_p$
• (3)
  • [1] $-\dfrac{1}{3}v_p$
  • [2] $0$
  • [3] $\dfrac{1}{3}v_p$
  • [4] $\dfrac{2}{3}v_p$
• (4)
  • [1] $2g(\sin\theta-\mu\cos\theta)$
  • [2] $2g(\sin\theta+\mu\cos\theta)$
  • [3] $g(\sin\theta-\mu\cos\theta)$
  • [4] $g(\sin\theta+\mu\cos\theta)$
• (5)
  • [1] $\mu\gt\tan\theta$
  • [2] $\mu\lt\tan\theta$
  • [3] $\mu\gt\dfrac{3}{4}\tan\theta$
  • [4] $\mu\gt\dfrac{1}{2}\tan\theta$
• (6)
  • [1] $-g\sin\theta$
  • [2] $-g\cos\theta$
  • [3] $g\sin\theta$
  • [4] $-g\cos\theta$
• (7)
  • [1] $-\dfrac{1}{3}v_p+gt\cos\theta$
  • [2] $-\dfrac{1}{3}v_p+gt\sin\theta$
  • [3] $\dfrac{1}{3}v_p-gt\cos\theta$
  • [4] $\dfrac{1}{3}v_p-gt\sin\theta$
• (8)
  • [1] $-\dfrac{1}{3}v_pt+\dfrac{1}{2}gt^2\sin\theta$
  • [2] $-\dfrac{1}{3}v_pt-\dfrac{1}{2}gt^2\sin\theta$
  • [3] $\dfrac{1}{3}v_pt+\dfrac{1}{2}gt^2\cos\theta$
  • [4] $\dfrac{1}{3}v_pt-\dfrac{1}{2}gt^2\sin\theta$
• (9)
  • [1] $-\dfrac{1}{3}v_p+gt(\sin\theta-\mu\cos\theta)$
  • [2] $\dfrac{1}{3}v_p+gt(\sin\theta-\mu\cos\theta)$
  • [3] $\dfrac{2}{3}v_p+gt(\sin\theta-\mu\cos\theta)$
  • [4] $\dfrac{2}{3}v_p-gt(\sin\theta-\mu\cos\theta)$
• (10)
  • [1] $\dfrac{1}{3}v_pt-\dfrac{1}{2}gt^2(\sin\theta-\mu\cos\theta)$
  • [2] $\dfrac{1}{3}v_pt+\dfrac{1}{2}gt^2(\sin\theta-\mu\cos\theta)$
  • [3] $\dfrac{2}{3}v_pt-\dfrac{1}{2}gt^2(\sin\theta-\mu\cos\theta)$
  • [4] $\dfrac{2}{3}v_pt+\dfrac{1}{2}gt^2(\sin\theta-\mu\cos\theta)$
• (11)
  • [1] $\dfrac{2}{3\mu g\cos\theta}v_p$
  • [2] $\dfrac{1}{\mu g\cos\theta}v_p$
  • [3] $\dfrac{3}{2\mu g\cos\theta}v_p$
  • [4] $\dfrac{2}{\mu g\cos\theta}v_p$