四酸化二窒素$(\text{N}_2\text{O}_4)$は、常温で一部が二酸化窒素$(\text{NO}_2)$に分解し、これらの間には次式のような化学平衡が成り立つ。 $$\text{N}_2\text{O}_4\leftrightarrows2\text{NO}_2\tag{A}\label{aa}$$

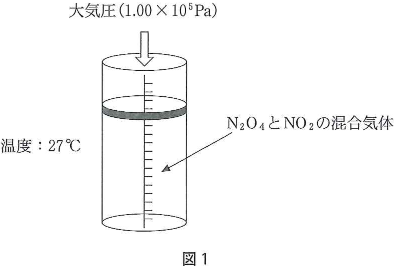
滑らかに動くピストンを備え、体積目盛を付けたシリンダー（図1）を用いて次の実験を行った。シリンダーの内部を18.4gの$\text{N}_2\text{O}_4$で満たした後、大気圧のもとで27℃に保った。シリンダー内の気体の体積が5.80Lになったところでピストンの動きが止まり、平衡状態に達したことがわかった。この結果に基づいて、下の問1～問8に答えよ。ただし、このときの大気圧は$1.00\times10^5$Paであり、ピストンの質量およびピストンとシリンダーの間の摩擦は無視できるものとする。また、気体は理想気体とみなし、気体定数は$R=8.30\times10^3$Pa・L/（K・mol）とし、原子量は$\text{N}=14.0$、$\text{O}=16.0$とする。

• 問1　シリンダーに入れた$\text{N}_2\text{O}_4$の物質量（mol）はいくらか。有効数字3桁で答えよ。
• 問2　平衡状態におけるシリンダー内の気体は$\text{N}_2\text{O}_4$と$\text{NO}_2$の混合気体である。この混合気体の全物質量（mol）はいくらか。次の（1）～（5）のうち最も近いものを選び、番号で答えよ。
  • （1）0.150
  • （2）0.182
  • （3）0.233
  • （4）0.312
  • （5）0.400
• 問3　平衡状態における混合気体中の$\text{N}_2\text{O}_4$の物質量（mol）はいくらか。次の（1）～（5）のうち最も近いものを選び、番号で答えよ。
  • （1）0.033
  • （2）0.066
  • （3）0.167
  • （4）0.200
  • （5）0.233
• 問4　平衡状態における混合気体中の$\text{N}_2\text{O}_4$のモル分率はいくらか。次の（1）～（5）のうち最も近いものを選び、番号で答えよ。
  • （1）0.142
  • （2）0.283
  • （3）0.576
  • （4）0.717
  • （5）0.835
• 問5　平衡状態における混合気体中の$\text{N}_2\text{O}_4$の分圧（Pa）はいくらか。次の（1）～（5）のうち最も近いものを選び、番号で答えよ。
  • （1）$1.42\times10^4$
  • （2）$2.83\times10^4$
  • （3）$5.76\times10^4$
  • （4）$7.17\times10^4$
  • （5）$8.35\times10^4$
• 問6　平衡状態における$\text{N}_2\text{O}_4$と$\text{NO}_2$の分圧をそれぞれ$p_1$および$p_2$として、$\eqref{aa}$式の反応の圧平衡定数$K_p$を$p_1$と$p_2$を用いて表せ。
• 問7　27℃における$\eqref{aa}$式の反応の圧平衡定数$K_p$（Pa）はいくらか。有効数字2桁で答えよ。
• 問8　ピストンに重りをのせて混合気体にかかる圧力を$2.00\times10^5$Paにすると、混合気体の体積はどのようになるか。次の（1）～（3）のうち正しいものを選び、番号で答えよ。
  • （1）混合気体は理想気体とみなされる。したがって、圧力が2倍になったため体積は1/2、すなわち、2.90Lになる。
  • （2）圧力が高くなると、（1）式の反応が右側に進行して新たな平衡状態に達するため混合気体の全物質量が増加する。したがって、体積は2.90Lよりも大きくなる。
  • （3）圧力が高くなると、（1）式の反応が左側に進行して新たな平衡状態に達するため混合気体の全物質量が減少する。したがって、体積は2.90Lよりも小さくなる。