図のように、球体とゴンドラからなる気球があり、ゴンドラに荷物が積んである。球体内にヒーターがあり、球体内の空気の温度を変化させることができる。球体の下部には穴があいており、そこでは球体内の空気の圧力は、つねに外気の圧力に等しい。この気球と積荷の質量はあわせて$3.0\times10^2$kgである（球体内の空気の質量は含まない）。球体は薄い素材で作られていて、その体積はつねに$1.0\times10^3$m³である。地表における外気の温度と密度は、それぞれ$3.0\times10^2$K、1.2kg/m³である。空気は理想気体とみなせ、ゴンドラ、積荷、およびヒーターの体積は無視できるとし、重力加速度の大きさを10m/s²として、以下の文中の空欄内に入れるのに適当なものを解答群の中からひとつ選び、その番号を解答欄に記入せよ。

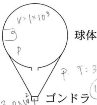
はじめ、気球は地表で静止しており、球体内の気温と外気の温度は等しいとする。このとき、気球と積荷にはたらく重力は$\fbox{1}$N、球体内の空気にはたらく重力は$\fbox{2}$N、気球にはたらく浮力は$\fbox{3}$Nである。

ヒーターによって球体内の空気を加熱すると、ある温度になったところで気球は上昇し始める。このとき、気球にはたらく浮力は$\fbox{4}$N、気球と積荷にはたらく重力は$\fbox{1}$N、球体内の空気にはたらく重力は$\fbox{5}$Nであり、球体内の空気の温度は$\fbox{6}$Kである。また、球体内の空気の密度は$\fbox{7}$kg/m³である。

ヒーターの出力が弱く、球体内の空気を$\fbox{6}$Kより40Kだけ低い温度までしか加熱できないとする。この温度まで加熱したときの球体内の空気の密度は$\fbox{8}$kg/m³であり、球体内の空気にはたらく重力は$\fbox{9}$Nである。気球が浮かび上がるためには、$\fbox{10}$kg以上の積荷を減らす必要がある。

• [11] 0.10
• [12] 0.12
• [13] 0.20
• [14] 0.30
• [15] 0.40
• [16] 0.50
• [17] 0.60
• [18] 0.90
• [19] 1.0
• [20] 1.2
• [21] 2.0
• [22] 3.0
• [23] 4.0
• [24] 5.0
• [25] 6.0
• [26] 9.0
• [27] 10
• [28] 12
• [29] 20
• [30] 30
• [31] 40
• [32] 50
• [33] 60
• [34] 90
• [35] $1.0\times10^2$
• [36] $1.2\times10^2$
• [37] $2.0\times10^2$
• [38] $3.0\times10^2$
• [39] $4.0\times10^2$
• [40] $5.0\times10^2$
• [41] $6.0\times10^2$
• [42] $9.0\times10^2$
• [43] $1.0\times10^3$
• [44] $1.2\times10^3$
• [45] $2.0\times10^3$
• [46] $3.0\times10^3$
• [47] $4.0\times10^3$
• [48] $5.0\times10^3$
• [49] $6.0\times10^3$
• [50] $9.0\times10^3$
• [51] $1.0\times10^4$
• [52] $1.2\times10^4$
• [53] $2.0\times10^4$
• [54] $3.0\times10^4$
• [55] $4.0\times10^4$
• [56] $5.0\times10^4$
• [57] $6.0\times10^4$
• [58] $9.0\times10^4$