自治医科大学物理2012年第5セット

地面からの高さ$h$の位置から小さな鉄球を自由落下させたところ、鉄球は地中$d$の深さまでめり込み静止した。鉄球が地面に到達してから静止するまでの平均の加速度はいくらか。ただし、重力加速度の大きさを$g$とし、空気抵抗は無視できるものとする。
- (ア) $\dfrac{1}{2}\dfrac{gh}{d}$
- (イ) $\dfrac{1}{\sqrt{2}}\dfrac{gh}{d}$
- (ウ) $\dfrac{gh}{d}$
- (エ) $\sqrt{2}\dfrac{gh}{d}$
- (オ) $2\dfrac{gh}{d}$
ばね定数$k$の軽いばねに質量$m$のおもりをつるすと、ばねが$l$伸びて静止した。この状態からおもりを手で静かに自然の長さになるまで鉛直上向きに押し上げた。手がおもりにした仕事はいくらか。重力加速度の大きさを$g$とする。
- (ア) 0
- (イ) $mgl$
- (ウ) $\dfrac{1}{2}kl^2$
- (エ) $mgl+\dfrac{1}{2}kl^2$
- (オ) $mgl-\dfrac{1}{2}kl^2$
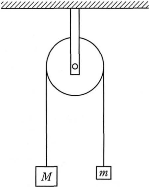
図のように定滑車を天井につけ、軽い糸をかけ、その両端に質量$M$、$m$ $(M\gt m)$である物体をつるして手をはなした。このとき、定滑車が天井を引く力の大きさはいくらか。ただし、滑車はなめらかに回転するものとし、定滑車の質量は無視できるとする。また重力加速度の大きさを$g$とする。
- (ア) $(M+m)g$
- (イ) $\dfrac{(M+m)^2}{M-m}g$
- (ウ) $\dfrac{(M-m)^2}{M+m}g$
- (エ) $\dfrac{2Mm}{M+m}g$
- (オ) $\dfrac{4Mm}{M+m}g$
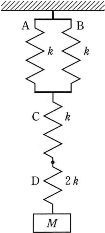
図のように、自然長の等しい軽いばねA、B、C、Dをつなぎ、上部を天井に固定する。最下部に質量$M$のおもりをぶら下げ静止させる。A、B、Cのばね定数は$k$で、Dのばね定数は$2k$である。また、AとBは伸びが同じになるように上下を固定具でつないである。Dに蓄えられる弾性エネルギーは、Aに蓄えられる弾性エネルギーの何倍か。
- (ア) $\dfrac{1}{4}$
- (イ) $\dfrac{1}{2}$
- (ウ) $1$
- (エ) $2$
- (オ) $4$
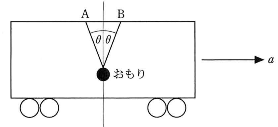
図のように、水平右向きに一定の加速度$a$で運動している電車の水平な天井の2点A、Bから軽い同じ長さの糸でおもりをつり下げる。糸がたるまないでいられる$a$の大きさの最大値はいくらか。ただし、AとBを結ぶ直線は電車の運動方向と同じ向きで、静止しているときの糸と鉛直方向のなす角度を$\theta$とし、おもりの大きさは無視できるものとする。また重力加速度の大きさを$g$とする。
- (ア) $g\sin\theta$
- (イ) $g\tan\theta$
- (ウ) $g(1-\cos\theta)$
- (エ) $g\sin\theta\cos\theta$
- (オ) $g\dfrac{\tan\theta}{1+\tan\theta}$
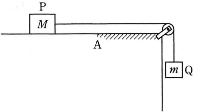
図のように、水平面に置いた質量$M$の物体Pに軽い糸をつけ、軽い定滑車を通して他端に質量$m$の物体Qをつり下げたところ、2つの物体は動き始めた。水平面上のAから左の部分はなめらかであるが、右の部分はあらい水平面で物体Pとの動摩擦係数は$\mu'$である。物体Pはなめらかな水平面を$l_1$だけすべりAに達し、Aから$l_2$だけすべって停止した。動摩擦係数$\mu'$はいくらか。
ただし、Pと滑車の間の糸は水平で、物体の大きさは無視できるものとする。
- (ア) $\dfrac{m}{M}\bigg(\dfrac{l_1}{l_2}\bigg)$
- (イ) $\dfrac{m}{M}\bigg(\dfrac{l_2}{l_1}\bigg)$
- (ウ) $\dfrac{m}{M}\bigg(\dfrac{l_1+l_2}{l_1}\bigg)$
- (エ) $\dfrac{m}{M}\bigg(\dfrac{l_1+l_2}{l_2}\bigg)$
- (オ) $\dfrac{m}{M}\bigg(\dfrac{l_1}{l_1+l_2}\bigg)$