四角に適する解答をマークせよ。
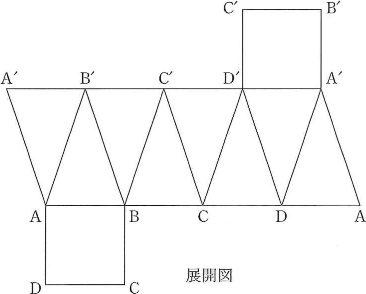
空間に一辺の長さが2の2つの正方形$\text{S}:\text{ABCD}$、$\text{S'}:\text{A'B'C'D'}$がある。$\text{S}$、$\text{S'}$の対角線の交点をそれぞれ$\text{O}$、$\text{O'}$とし、$\text{OO'}$はそれぞれの面と直交し、長さは3とする。さらに、$\overrightarrow{\text{OA}}$と$\overrightarrow{\text{O'A'}}$のなす角は$\dfrac{1}{4}\pi$であり、$\overrightarrow{\text{OA}}$と$\overrightarrow{\text{O'B'}}$のなす角は$\dfrac{1}{4}\pi$である。このとき、2つの正方形を8つの線分$\text{AA'}$、$\text{AB'}$、$\text{BB'}$、$\text{BC'}$、$\text{CC'}$、$\text{CD'}$、$\text{DD'}$、$\text{DA'}$で結び、底面が$\text{S}$と$\text{S'}$で、側面が8つの二等辺三角形からなる立体を考える。この立体の体積を求めてみよう。
底面$\text{S}$から高さ$h$の面で切ったこの立体の断面$\text{S}_h$の面積を$S(h)$とし、軸$\text{OO'}$と断面$\text{S}_h$の交点を$\text{O}_h$とする。
$\triangle{\text{AA'B'}}$と断面$\text{S}_h$の交線$l_h$に注目する。$\text{O}_h$から$l_h$の距離は$h$が0から3まで増加するとき$a=\sqrt{\fbox{ア}}-\fbox{イ}$だけ減少するので、$O_h$から$l_h$の距離の$h$に対する増加率は$\dfrac{\fbox{ウエ}}{\fbox{オ}}a$となり、また線分$l_h$の長さは$\dfrac{\fbox{カ}}{\fbox{キ}}h$である。同様に$\triangle{\text{B'AB}}$と断面$\text{S}_h$の交線について考えると$\text{O}_h$との距離の$h$に対する増加率は$\dfrac{\fbox{ク}}{\fbox{ケ}}a$となり線分の長さは$\dfrac{\fbox{コサ}}{\fbox{シ}}h+\fbox{ス}$となるので、$h$の増分を$\Delta h$とおいた時、面積の増分$\Delta\text{S}$は$\left(\dfrac{\fbox{セトタ}}{\fbox{チ}}h+\dfrac{\fbox{ツ}}{\fbox{テ}}\right)a\Delta h$となる。$S(0)=\fbox{ト}$を考慮すると、$S(h)=\left(\dfrac{\fbox{ナニ}}{\fbox{ヌ}}h^2+\dfrac{\fbox{ネ}}{\fbox{ノ}}h\right)a+\fbox{ハ}$となる。
この$S(h)$を0から3まで積分するとこの立体の体積は
$\fbox{ヒ}a+\fbox{フヘ}=\fbox{ホ}\sqrt{\fbox{マ}}+\fbox{ミ}$となる。