順天堂大学物理2013年第1問

次の問い(問1~問5)に答えよ。〔解答番号$\fbox{1}$~$\fbox{8}$〕

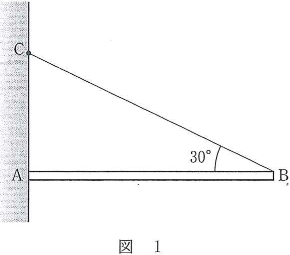
問1 図1のように、一様な棒$\text{AB}$の一方の端$\text{B}$を鉛直な壁の点$\text{C}$と糸でつなぎ、他方の端$\text{A}$を鉛直な壁に沿って動かし、$\text{AB}$が水平になるようにつり合わせた。このとき、$\text{BC}$をつなぐ糸と水平な棒$\text{AB}$のなす角の大きさは$30^\circ$になった。壁と棒の間の静止摩擦係数を$\mu$とすると、つり合いが保たれているためには \[\mu\geqq\fbox{1}\] の関係が成り立たなければならない。$\fbox{1}$に入れる数値として正しいものを、下の(1)~(8)のうちから一つ選べ。
- (1) $\dfrac{1}{4}$
- (2) $\dfrac{1}{3}$
- (3) $\dfrac{1}{2}$
- (4) $\dfrac{\sqrt{3}}{4}$
- (5) $\dfrac{\sqrt{2}}{3}$
- (6) $\dfrac{\sqrt{3}}{3}$
- (7) $\dfrac{\sqrt{2}}{2}$
- (8) $\dfrac{\sqrt{3}}{2}$
問2 真空中の波長が$\lambda$であるレーザー光を用いた干渉実験について、次の問い(a)、(b)に答えよ。
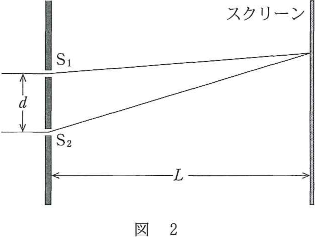
- (a) このレーザー光を、空気中で図2のように、間隔$d$の2本のスリット$\text{S}_1$、$\text{S}_2$をもつスリット板に垂直に入射させた。スリット板に平行で距離$L$の位置にあるスクリーン上にはスリット$\text{S}_1$、$\text{S}_2$からでた光の干渉により明暗の縞模様ができる。スクリーン上の明るい線の間隔はどのように表されるか。正しいものを、下の(1)~(6)のうちから一つ選べ。ただし、$L$は$d$に比べてじゅうぶん大きく、空気の屈折率は1としてよい。$\fbox{2}$
  - (1) $\dfrac{Ld}{2\lambda}$
  - (2) $\dfrac{L\lambda}{2d}$
  - (3) $\dfrac{Ld}{\lambda}$
  - (4) $\dfrac{L\lambda}{d}$
  - (5) $\dfrac{3Ld}{2\lambda}$
  - (6) $\dfrac{3L\lambda}{2d}$
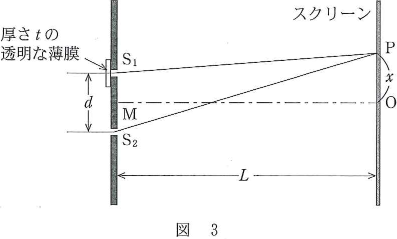
- (b) 次に、図3のように、スリット$\text{S}_1$を、屈折率$n$、厚さ$t$の透明な薄膜でおおう。薄膜でおおう前は、$\text{S}_1\text{S}_2$の中点$\text{M}$を通りスクリーンに垂直な直線とスクリーンとの交点$\text{O}$には縞模様の中心である明るい線がある。この明るい線は、スリット$\text{S}_1$を薄膜でおおうと、点$\text{O}$から$x$だけ離れた点$\text{P}$に移動した。$x$を表す式として正しいものを、下の(1)~(8)のうちから一つ選べ。$\fbox{3}$
  - (1) $\dfrac{(n-1)tL}{\lambda}$
  - (2) $\dfrac{(n-1)tL}{2\lambda}$
  - (3) $\dfrac{(n-1)tL}{n\lambda}$
  - (4) $\dfrac{(n-1)tL}{2n\lambda}$
  - (5) $\dfrac{(n-1)tL}{d}$
  - (6) $\dfrac{(n-1)tL}{2d}$
  - (7) $\dfrac{(n-1)tL}{nd}$
  - (8) $\dfrac{(n-1)tL}{2nd}$
問3 たくさんの水素分子がすべて同じ向きに同じ速さ$1.8\times 10^3$m/sで進み、固定した板の面と弾性衝突する。毎秒$7.0\times 10^{20}$個の分子が板の面の法線に対して$45^\circ$の角度で、面積$3.0$cm²の平らな板の面に一様に当たっているとする。この水素分子の流れが板の面におよぼす圧力はいくらか。最も近い値を、次の(1)~(9)のうちから一つ選べ。ただし、水素分子の分子量を$2.0$、アボガドロ定数を$6.0\times 10^{23}$/molとし、水素分子どうしの衝突はないものとする。また、$\sqrt{2}\fallingdotseq1.4$として計算してよい。$\fbox{4}$Pa
- (1) $10$
- (2) $20$
- (3) $30$
- (4) $40$
- (5) $50$
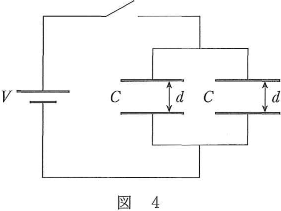
問4図4のように、空気中で極板間の距離$d$、電気容量$C$の二つの平行板コンデンサーがスイッチと電圧$V$の電池につながれている。下の問い[(a)、(b)]に答えよ。
- (a) スイッチを閉じて、二つのコンデンサーのうちの一つの極板間の距離を$2d$にひろげた。二つのコンデンサーに蓄えられた電気量の和はいくらか。正しいものを、次の(1)~(9)のうちから一つ選べ。$\fbox{5}$
  - (1) $CV$
  - (2) $2CV$
  - (3) $3CV$
  - (4) $\dfrac{1}{2}CV$
  - (5) $\dfrac{3}{2}CV$
  - (6) $\dfrac{5}{2}CV$
  - (7) $\dfrac{1}{4}CV$
  - (8) $\dfrac{3}{4}CV$
  - (9) $\dfrac{5}{4}CV$
- (b) 次にスイッチを切り、極板間の距離が$2d$のコンデンサーを元の距離$d$までゆっくりともどした。このとき、外力がする仕事はいくらか。正しいものを、次の(1)~(9)のうちから一つ選べ。$\fbox{6}$
  - (1) $-\dfrac{3}{4}CV^2$
  - (2) $-\dfrac{5}{4}CV^2$
  - (3) $-\dfrac{7}{4}CV^2$
  - (4) $-\dfrac{3}{8}CV^2$
  - (5) $-\dfrac{5}{8}CV^2$
  - (6) $-\dfrac{7}{8}CV^2$
  - (7) $-\dfrac{3}{16}CV^2$
  - (8) $-\dfrac{5}{16}CV^2$
  - (9) $-\dfrac{7}{16}CV^2$
問5 電子とイオンが電界中を移動する場合を考え、次の問い((a)、(b))に答えよ。
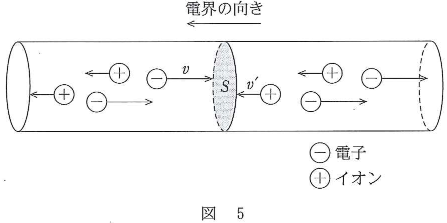
- (a) 負電荷$-e(e\gt 0)$をもつ電子は抵抗を受けながら一定の速さ$v$で図5のように電界と逆向きに移動し、正電荷$q$をもつイオンは一定の速さ$v’$で電界の向きに移動しているとする。電子とイオンは、それぞれ単位体積あたり$n$個、$n’$個で分布しているとする。電界に垂直な面積$S$の面を流れる電流はいくらか。正しいものを、下の(1)~(8)のうちから一つ選べ。ただし、電界の向きに流れる電流を正とする。$\fbox{7}$
  - (1) $envS$
  - (2) $qn’v’S$
  - (3) $-envS$
  - (4) $-qn’v’S$
  - (5) $(env+qn’v’)S$
  - (6) $(-env+qn’v’)S$
  - (7) $(env-qn’v’)S$
  - (8) $(-env-qn’v’)S$
- (b) オーロラに大電流が流れると、地上の送電・発電施設に大電流が流れ停電事故を引き起こすことがある。オーロラの中では大量の電子やイオンが図5のように移動していて、一定の電流が流れると仮定する。オーロラ中に$100$kVの電圧で$1\times 10^6$Aの電流が流れるときの電力はいくらか。正しいものを、次の(1)~(6)のうちから一つ選べ。$\fbox{8}$W
  - (1) $5\times 10^{10}$
  - (2) $1\times 10^{11}$
  - (3) $5\times 10^{14}$
  - (4) $1\times 10^{15}$
  - (5) $5\times 10^{15}$
  - (6) $1\times 10^{16}$