A まず一様磁界中に入射してきた荷電粒子の運動を考えよう。磁束密度の大きさを$B$として、次の問い(問1~問3)に答えよ。

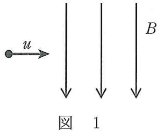
• 問1 図1のように、質量$m$、電荷$q(q\gt 0)$の荷電粒子が磁界に垂直な向きに速さ$u$で入射すると、磁界に垂直な面で等速円運動をする。この円運動の半径として正しいものを、下の(1)~(9)のうちから一つ選べ。$\fbox{1}$
  
  • (1) $quB$
  • (2) $\dfrac{qB}{m}$
  • (3) $\dfrac{qB}{mu}$
  • (4) $\dfrac{qB}{mu^2}$
  • (5) $\dfrac{qB^2}{mu}$
  • (6) $\dfrac{m}{qB}$
  • (7) $\dfrac{mu}{qB}$
  • (8) $\dfrac{mu}{qB^2}$
  • (9) $\dfrac{mu^2}{qB}$
• 問2 前問の円運動の軌道に囲まれた磁束として正しいものを、次の(1)~(9)のうちから一つ選べ。$\fbox{2}$
  • (1) $B$
  • (2) $2\pi quB^2$
  • (3) $\pi q^2u^2B^3$
  • (4) $\dfrac{2\pi mB}{qu}$
  • (5) $\dfrac{2\pi muB}{q}$
  • (6) $\dfrac{2\pi qB^2}{mu}$
  • (7) $\dfrac{\pi q^2B^3}{m^2u^2}$
  • (8) $\dfrac{\pi m^2u^2}{q^2B}$
  • (9) $\dfrac{\pi m^2u^2}{q^2B^2}$
• 問3 正電荷$q$、質量$m$の粒子と負電荷$-q$、質量$m’$の粒子が、同じ速度で磁界の向きに対して斜めに入射し、らせん運動をしながら移動しているとする。図2のア~エは、磁束密度$B$の磁界中の荷電粒子のらせん運動の軌道である。軌道上の矢印は、らせん運動の回転の向きである。荷電粒子の質量が$m\gt m’$の条件をみたすとき、それぞれのらせん運動の特徴を表すものとして正しい組み合わせを、下の(1)~(10)のうちから一つ選べ。
  (正電荷粒子の軌道、負電荷粒子の軌道)=$\fbox{3}$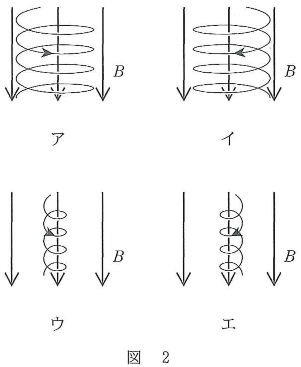
  
  • (1) (ア、イ)
  • (2) (ア、ウ)
  • (3) (ア、エ)
  • (4) (イ、ア)
  • (5) (イ、ウ)
  • (6) (イ、エ)
  • (7) (ウ、ア)
  • (8) (ウ、イ)
  • (9) (エ、ア)
  • (10) (エ、イ)

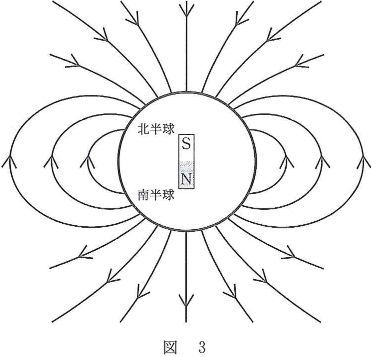
B 地球のまわりには、図3のように地球が大きな棒磁石であるような磁界ができている。それは前問Aのような一様磁界とは異なり、地表に近づくほど磁力線が密になっていく磁界である。この磁界中の荷電粒子の運動について、下の問い(問4~問6)に答えよ。

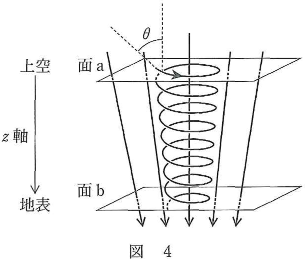
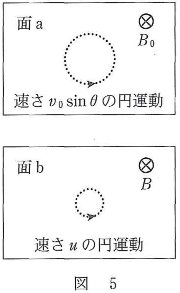
• 問4 北半球の地表付近の磁界中の荷電粒子の運動を考えよう。図4のように、地表に向かう下向きを$z$軸方向とし、$z$軸に垂直な面を面$a$、面$b$とする。荷電粒子が速さ$v_0$で面$a$を$z$軸に対して角度$\theta$の向きに通過して、らせん軌道を描きながら地表に近い面$b$に達する。このらせん軌道は、$z$方向の運動と、$z$軸に垂直な面内の円運動(図5)に分けて考えることができる。磁界の変化はじゅうぶんゆるやかなので、図5の面$a$、面$b$内の円運動は、それぞれ、$z$方向の磁束密度$B_0$、$B$の一様磁界中の速さ$v_0\sin\theta$、$u$の等速円運動としてよいとする。電磁誘導の法則から磁束の変化は妨げられるので、地表に近づいて磁束密度が大きくなると円運動の半径が小さくなり、円軌道に囲まれた磁束が一定に保たれることが知られている。このことを用いて、面$b$における速さ$u$を表す式として正しいものを、下の(1)~(8)のうちから一つ選べ。$u=\fbox{4}$
  
  
  • (1) $\sqrt{\dfrac{B_0}{B}}v_0\sin\theta$
  • (2) $\sqrt{\dfrac{B}{B_0}}v_0\sin\theta$
  • (3) $\dfrac{B_0}{B}v_0\sin\theta$
  • (4) $\dfrac{B}{B_0}v_0\sin\theta$
  • (5) $\left(\dfrac{B_0}{B}\right)^\frac{3}{2}v_0\sin\theta$
  • (6) $\left(\dfrac{B}{B_0}\right)^\frac{3}{2}v_0\sin\theta$
  • (7) $\left(\dfrac{B_0}{B}\right)^2v_0\sin\theta$
  • (8) $\left(\dfrac{B}{B_0}\right)^2v_0\sin\theta$
• 問5 磁力線は図4のように地表近くで密に集まってくるため、荷電粒子にはたらくローレンツ力に負の$z$成分が生じる。荷電粒子は速度の$z$成分が小さくなりやがてゼロとなる面で反射され、らせん軌道を描きながら地表から遠ざかる。磁界は荷電粒子に仕事をしないので運動エネルギーは一定である。前問4の荷電粒子が面$a$の位置で入射し面$b$の位置で反射されるとしたとき、入射したときと反射されたときの荷電粒子の運動エネルギーが等しいことから、反射される位置の磁束密度の大きさがわかる。反射される位置の磁束密度の大きさとして正しいものを、次の(1)~(10)のうちから一つ選べ。$\fbox{5}$
  • (1) $B_0\sqrt{v_0\sin\theta}$
  • (2) $B_0v_0\sin\theta$
  • (3) $B_0(v_0\sin\theta)^2$
  • (4) $\dfrac{B_0}{v_0\sin\theta}$
  • (5) $\dfrac{B_0}{(v_0\sin\theta)^2}$
  • (6) $B_0\sqrt{\sin\theta}$
  • (7) $B_0\sin\theta$
  • (8) $B_0\sin^2\theta$
  • (9) $\dfrac{B_0}{\sin\theta}$
  • (10) $\dfrac{B_0}{\sin^2\theta}$
• 問6 オーロラは、太陽から飛来した荷電粒子が地球の磁力線に沿ってらせん運動をしながら磁界の強い所に集まり、大気の分子と衝突して発光し、さまざまな色や形の光のカーテンを作る電磁現象である。図3で与えられる地球の磁界の様子と問4及び問5から導かれることとして、正しくないものを次の(1)~(5)のうちから一つ選べ。$\fbox{6}$
  • (1) 地表から遠い面$a$内の円運動の周期は、地表に近い面$b$内の円運動の周期よりも小さい。
  • (2) 南半球でも荷電粒子が反射される位置があり、反射された粒子は磁力線に沿って北半球へ向かって移動する。
  • (3) 南北を結ぶ磁力線に沿って往復するたくさんの荷電粒子が、北半球と南半球にオーロラを作ることがある。
  • (4) 面$a$で入射した荷電粒子が反射される面の位置は、入射の速さ$v_0$には依存しない。
  • (5) 磁力線の形状から、赤道では大気に侵入してくる荷電粒子が少ないため、高緯度地帯に比べてオーロラは発生しにくい。