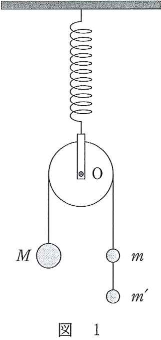
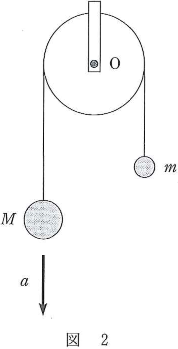
図1のように、ばね定数$k$のばねの一端を天井に固定して、他端を回転軸$\text{O}$のまわりに滑らかに回る滑車に取りつける。滑車には糸が通してあり、糸の端には質量$M$のおもり、他方の端には質量$m$、$m’$の二つのおもりがつながれて、おもりも滑車もつり合いの状態で静止している。重力加速度の大きさを$g$とし、糸はじゅうぶん長く、また、糸の質量と滑車の質量は無視できるとして、下の問い(問1~問6)に答えよ。

• 問1 図1のつり合いの状態におけるばねの自然長からの伸びを求めよ。ただし、答えは$M$、$g$、$k$を用いて表せ。
• 問2 図1の質量$m$と質量$m’$のおもりをつなぐ糸を切ると、おもりと滑車は運動を始める。滑車の回転軸$\text{O}$が大きさ$\beta$の上向きの加速度で動いているときの糸の張力は$S$とし、質量$M$のおもりは、$\text{O}$から見て下向きの加速度$a$をもつとする(図2)。質量$M$と質量$m$の二つのおもりそれぞれに対する運動方程式を求めよ。ただし、答えは$M$、$m$、$g$、$a$、$\beta$、$S$のうちから必要なものを用いて表せ。
• 問3 前問の運動方程式から、糸の張力$S$と$\text{O}$から見たおもりの加速度$a$を求めよ。ただし、答えは$M$、$m$、$g$、$\beta$を用いて表せ。
• 問4 滑車の質量を無視しているので、滑車にはたらくばねの弾性力と滑車が糸から受ける力はつり合う。ばねの伸びを$x$としたとき、糸の張力$S$を$k$、$x$を用いて表せ。
• 問5 糸がたるまないとき、滑車は単振動することがわかる。この単振動の周期を求めよ。ただし、答えは$M$、$m$、$g$、$k$のうちから必要なものを用いて表せ。
• 問6 糸がたるまずに単振動するという条件から、$M$と$m$の間に成り立つ不等式を求めよ。ただし、答えは$M$、$m$を用いて表せ。