順天堂大学物理2012年第3問
熱を通さないシリンダーと、熱を通さない断面積$S$、質量$M$のピストンがある。シリンダーとピストンの間から気体はもれず、ピストンはなめらかに動くものとする。シリンダー内部には圧力$p$、温度$T$の理想気体があり、ピストンはシリンダーの底面から高さ$L$で静止している(図1)。気体の定積モル比熱を$C_V$、重力加速度の大きさを$g$、気体定数を$R$、外気の大気圧は無視できるものとして、下の問い(問1~問5)に答えよ。
〔解答番号$\fbox{1}$~$\fbox{5}$〕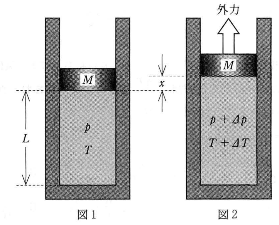
〔解答番号$\fbox{1}$~$\fbox{5}$〕

- 問 1 図1のように、ピストンにはたらく重力と気体の圧力による力がつり合っているとき、シリンダー内部の気体の圧力$p$はいくらか。正しいものを、次の(1)~(6)のうちから一つ選べ。
$p=\fbox{1}$- (1) $Mg$
- (2) $MgL$
- (3) $MgS$
- (4) $\dfrac{Mg}{S}$
- (5) $\dfrac{Mg}{L}$
- (6) $\dfrac{Mg}{LS}$
- 問 2 ピストンが静止している状態から、ピストンに外力を加えてわずかな距離$x$だけ持ち上げたところ(図2)、理想気体の圧力と温度は、それぞれ、$p+\Delta p$、$T+\Delta T$になった。状態方程式を用いると、圧力の変化の割合$\dfrac{\Delta p}{p}$と温度の変化の割合$\dfrac{\Delta T}{T}$の間には、$\dfrac{\Delta p}{p}=\fbox{2}$の関係がある。$\fbox{2}$に入れるのに正しい式を、次の(1)~(8)のうちから一つ選べ。ただし、$a$、$b$が1に対してじゅうぶん小さいとき、$(1+a)(1+b) \fallingdotseq 1+a+b$と近似してよい。
- (1) $\dfrac{\Delta T}{T}+\dfrac{x}{L}$
- (2) $\dfrac{\Delta T}{T}-\dfrac{x}{L}$
- (3) $\dfrac{\Delta T}{T}+\dfrac{xL}{S}$
- (4) $\dfrac{\Delta T}{T}-\dfrac{xL}{S}$
- (5) $-\dfrac{\Delta T}{T}+\dfrac{x}{L}$
- (6) $-\dfrac{\Delta T}{T}-\dfrac{x}{L}$
- (7) $-\dfrac{\Delta T}{T}+\dfrac{xL}{S}$
- (8) $-\dfrac{\Delta T}{T}-\dfrac{xL}{S}$
- 問 3 熱の出入りはないので、ピストンを$x$だけ持ち上げると気体は断熱変化する。このとき温度変化の割合$\dfrac{\Delta T}{T}$はどのように表されるか。正しいものを、次の(1)~(8)のうちから一つ選べ。
$\dfrac{\Delta T}{T}=\fbox{3}$- (1) $-\dfrac{R}{C_VL}x$
- (2) $\dfrac{R}{C_VL}x$
- (3) $-\dfrac{C_V}{RL}x$
- (4) $\dfrac{C_V}{RL}x$
- (5) $-\dfrac{R}{(C_V+R)L}x$
- (6) $\dfrac{R}{(C_V+R)L}x$
- (7) $-\dfrac{C_V+R}{RL}x$
- (8) $\dfrac{C_V+R}{RL}x$
- 問 4 このときピストンに加えている鉛直方向の外力の大きさはいくらか。正しいものを、次の(1)~(8)のうちから一つ選べ。$\fbox{4}$
- (1) $\dfrac{RMg}{C_VL}x$
- (2) $\dfrac{RMgL}{C_VS}x$
- (3) $\dfrac{C_VMg}{RL}x$
- (4) $\dfrac{C_VMgL}{RS}x$
- (5) $\dfrac{C_VMg}{(C_V+R)L}x$
- (6) $\dfrac{C_VMgL}{(C_V+R)S}x$
- (7) $\dfrac{(C_V+R)Mg}{C_VL}x$
- (8) $\dfrac{(C_V+R)MgL}{C_VS}x$
- 問 5 ピストンに加えていた外力を取り去れば、ピストンは単振動を始める。このときの単振動の周期はいくらか。正しいものを、次の(1)~(8)のうちから一つ選べ。$\fbox{5}$
- (1) $2\pi\sqrt{\dfrac{C_VL}{gR}}$
- (2) $2\pi\sqrt{\dfrac{C_VS}{gLR}}$
- (3) $2\pi\sqrt{\dfrac{RL}{gC_V}}$
- (4) $2\pi\sqrt{\dfrac{RS}{gC_VL}}$
- (5) $2\pi\sqrt{\dfrac{(C_V+R)L}{gC_V}}$
- (6) $2\pi\sqrt{\dfrac{(C_V+R)S}{gC_VL}}$
- (7) $2\pi\sqrt{\dfrac{C_VL}{g(C_V+R)}}$
- (8) $2\pi\sqrt{\dfrac{C_VS}{g(C_V+R)L}}$