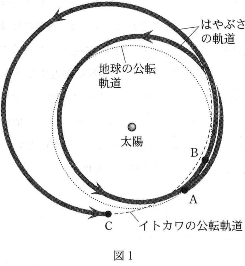
小惑星探査機「はやぶさ」は、小惑星イトカワの砂を持ち帰って来た。図1の太線ははやぶさの軌道で、地球の公転軌道上の点Aで地球を出発し、イトカワの公転軌道上の点Cでイトカワの砂を採取して地球に帰ってきた。点Aから点C までの運動について下の問い(問1～間3)に答えよ。

• 問 1 はやぶさはロケットに格納され、図1の点Aで地球から打ち上げられた。ロケットエンジンは燃料を噴射すると、その逆方向にロケットが進む力を与える。次の問い((a)、(b))に答えよ。
  • (a) 鉛直上向きにロケットを加速したとき、エンジンが与える力の大きさを$F$、上向きの加速度を$a$、ロケットの質量を$M$、重力加速度の大きさを$g$として運動方程式を書け。ただし、空気抵抗は無視する。
  • (b) 打ち上げられてから10秒後のロケットの速さは時速何kmか。ただしこの間、$F$と$M$の値は変化しないと仮定し、$F=4.0\times10^6~\text{N}$、$M=2.0\times10^5~\text{kg}$、$g=9.8~\text{m/s}^2$として、有効数字2桁で求めよ。
• 問 2 図1の点Aでロケット先端部から飛び出したはやぶさは、地球の公転軌道の近くを地球の後追いをするように太線に沿って太陽のまわりを1周した。そしてイトカワへ向かう新たな軌道に乗るため、図1の点Bで再び地球に接近して、燃料を使わずに速度を上げることのできる「地球スウィングバイ」という航法を行った。次の問い((a)、(b))に答えよ。
  • (a) まず、このスウィングバイを地球の観測者が見た様子を考えてみよう。図2のように、地球に接近してきたはやぶさは、地球に最接近してから方向を変えて地球を遠ざかってゆく。地球の中心からじゅうぶん離れた距離$r_0$の位置におけるはやぶさの速度を、地球に接近するときと遠ざかるとき、それぞれ$\vec{u_i}$と$\vec{u_f}$とする。スウィングバイの間、力学的エネルギーは保存するとしよう。このとき$|\vec{u_i}|=|\vec{u_f}|$が成り立つ。地球に最接近したときの速さ$|\vec{u_m}|$を、$r_0$、$\vec{u_i}$、地球の中心から最接近点までの距離$r_m$、地球の質量$M_E$、万有引力定数$G$を用いて表せ。

  • (b) 次に太陽から見た図2の様子を考えてみよう。図1の点Bで、はやぶさは地球の公転軌道からイトカワの公転軌道へ乗りうつる。このとき、はやぶさは地球の重力によって運動すると同時に、地球の公転運動に引っ張られて一気に速度を変える。図2の$\vec{u_i}$、$\vec{u_f}$を太陽から見ると$\vec{v_i}$、$\vec{v_f}$になるとする。ただしこの間、地球の公転の速度は一定とみなし、この速度を$\vec{V}$とする。

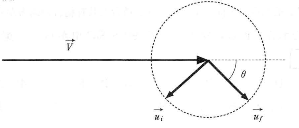
    では、$|\vec{v_f}|$が最大となるような$\vec{u_i}$、$\vec{u_f}$、$\vec{V}$の関係を求めてみよう。解答用紙に、$\vec{V}$と$\vec{u_f}$のなす角が$\theta$の場合の$\vec{u_i}$、$\vec{u_f}$、$\vec{V}$の関係が図示されている。この図に$\vec{v_i}$と$\vec{v_f}$を表すベクトルをかき加えよ。この図において、$|\vec{v_f}|$が最大となる$\theta$はいくらか。またこのときの$|\vec{v_f}|$の値を、$|\vec{V}|=30~\text{km/s}$、$|\vec{u_i}|=|\vec{u_f|}=4~\text{km/s}$とした場合に求めよ。

    (解答欄)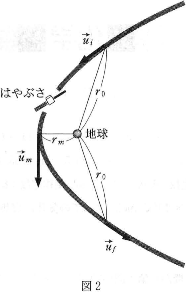
    
    
• 問 3 小惑星イ トカワも太陽の重力(万有引力)を向心力として公転している。イトカワの公転軌道を円軌道とみなしたとき、イトカワの公転周期$T$を、円軌道の半径$R$、太陽の質量$M_s$、万有引力定数$G$を用いて表せ。