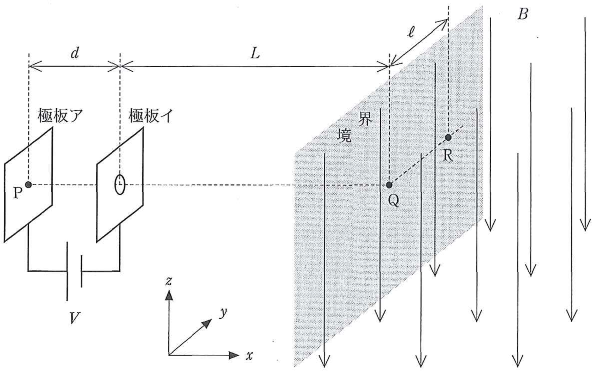
ア、イ2枚の薄い金属極板を、図のように距離$d$だけ隔てて$x$軸に垂直に置き、両者の間に大きさ$V$の電圧を印加する。極板イに面した極板ア上の点$\text{P}$を通り$x$軸に平行な直線が、極板イと交わる位置に小穴をあけ、さらにこの直線の延長上で、極板イからの距離が$L$となる位置を点$\text{Q}$とする。点$\text{Q}$を含み$yz$面に平行な平面を境界として、これより$x$座標の大きい領域には、図のように、$-z$方向に磁束密度$B$の一様な磁場が存在している。質量$m$と正電荷$q$を持つ荷電粒子を、初速度$0$で点$\text{P}$置いたとき、この荷電粒子の運動について以下の問に答えよ。重力の影響は無視できるものとする。途中の考え方も記せ。

• 問1 荷電粒子が極板ア、イの間で持つ加速度の大きさはいくらか。
• 問2 加速した荷電粒子が極板イの小穴を通過するときの速さはいくらか。
• 問3 極板イの小穴を通過した荷電粒子は、点$\text{Q}$を通って磁場中に入射した。荷電粒子が磁場中で受ける力の大きさはいくらか。
• 問4 磁場中に入射した荷電粒子は、点$\text{Q}$から$+y$方向に距離$l$だけ離れた点$\text{R}$に到達した。$l$の大きさはいくらか。
• 問5 荷電粒子が点$\text{Q}$を通過してから時間が$t_1$だけ経過した瞬間に、磁場の強さを変えずにその方向を1度だけ$+z$方向に反転させる。荷電粒子が磁場中から二度と出ないようにするために、$t_1$が満たさなければならない条件を求めよ。