関西医科大学物理2012年第1問

下の文を読んで、下記の(1)から(5)の問いに答えよ。ただし万有引力定数を$G$とする。また太陽の公転、自転の影響は無視してよいとする。

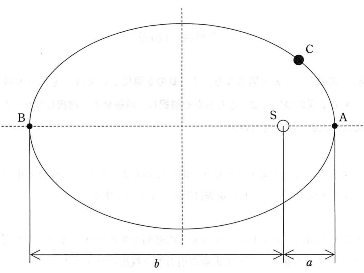
(1) 太陽S$($質量$M)$のまわりを半径$a$で円運動をする物体C(質量$m$)がある。この物体Cにある速度を与えて太陽の引力圏を脱出させようとしたとき、脱出に必要な最小速度$V_0$を求めよ。ただし簡単のために太陽の半径は$a$に比べて十分小さく、無視してよいとする。

次に、もっと一般的に太陽S(質量$M$)のまわりを物体C(質量$m$)がまわるための条件を考えてみよう。ケプラーの第一法則によれば、物体が太陽の引力圏から脱出しないときには図のような楕円軌道を描く。近日点(太陽に最も近い点)Aの太陽Sからの距離$a$、Aにおける速度$V_a$が与えられているとき、遠日点(太陽に最も遠い点)Bの太陽Sからの距離$b$を求めてみよう。簡単のために$a$に比べて太陽の半径は無視できるとする。
(2) 遠日点Bでの物体Cの速度を$V_b$とするとき、エネルギー保存則により$a$、$b$、$V_a$、$V_b$の間に成り立つ関係を求めよ。
(3) ケプラーの第二法則によれば、短い時間$\Delta t$の間に物体Cと太陽Sとを結ぶ線分(動径)が描く面積は一定である。この法則を用いて$a$、$b$、$V_a$、$V_b$の間に成り立つ関係を求めよ。
(4) (2)、(3)の関係を用いて、$b$を求めよ。
(5) 物体Cが太陽Sの周りを楕円運動をするためには、$V_a$は(1)で求めた$V_0$とどのような関係になければならないか。