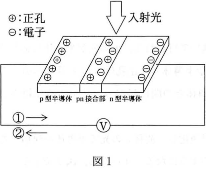
太陽光発電は図1のような原理に基いて行われる。太陽光が半導体にあたると、電子と正孔の対が生まれ、電子はn型半導体へ、正孔はp型半導体へ引き寄せられる。その結果n型半導体とp型半導体との間に起電力が発生する仕組みとなっている。

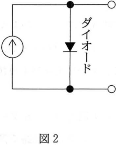
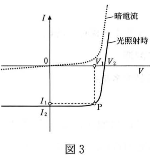
いま太陽光をフィルターを通して単色化し、波長$\lambda$の光で半導体を照射したとしよう。これを等価回路で書くと図2のようになる。すなわち、図2で下から上向きに一定の電流が流れる定電流源とダイオードの組み合わせと して書きあらわせる。電流－電圧特性は、図3のようになる。ここで点線で表したのは、光があたらないときの特性(暗電流)で、これはダイオードの特性に等しい。それに対し、光があたったときには、光量に比例した定電流が流れるために、電流－電圧特性は図3の実線のようになる。

• (1) 図1で回路を流れる電流は、左から右向き(図の電流1)か、右から左向き(図の電流2)か。理由を添えて答えよ。
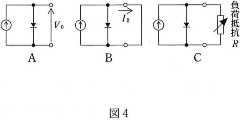
• (2) 図4の等価回路Aの$V_0$は図3のどの値にあたるか。下記の中から最も適当と思われる値を選び、その選択肢の前に付けられた記号を解答欄に記せ。ただし図4のAで、$V_0$は上方を正として定義されている。
  • (ア) $-V_2$
  • (イ) $-V_1$
  • (ウ) 0
  • (エ) $V_1$
  • (オ) $V_2$
• (3) 図4の等価回路Bの電流$I_0$は図3のどの値にあたるか。下記の中から最も適当と恩われる値を選び、その選択肢の前に付けられた記号を解答欄に記せ。ただし図4のBで、$I_0$は左から右に流れるときを正として定義されている。
  • (カ) $-I_2$
  • (キ) $-I_1$
  • (ク) 0
  • (ケ) $I_1$
  • (コ) $I_2$
• (4) 図4の等価回路Cのように、負荷抵抗$R$をつけたとき、図3の電流－電圧特性曲線上では、動作点は、P点の値になることが分かった。このとき、 この太陽電池の単位時間あたりの出力エネルギーはいくらになるか。
• (5) いま単位時間に太陽光の光量子が$n$個あたっている。このとき太陽電池の効率はいくらか。ただし太陽電池の効率とは、太陽から与えられた光のエネルギーのうち、どれだけのエネルギーが出力として取り出せるかを示すものである。