(1) 質量$m$の物体が、$x$軸上を正の方向に進む直線運動を考える。物体の進む先に、微小な幅$\Delta x$を有する特別な区間が$n$か所あり、物体が通過する順にそれぞれ区間1、区間2、$\cdots$、区間$n$とする。物体には、各区間を通過する間のみ、$x$軸の方向に一定の力$F_1,F_2,\cdots,F_n$がかかり、それ以外の場所では物体に力は働かないものとする。

区間1に進入する前の物体の速度が$v_0$のとき、区間1を通過した直後の物体の速度$v_1$は、$v_1=\fbox{ア}$で、区間1を通過するのにかかる時間$\Delta t_1$は、$\Delta t_1=\fbox{イ}$である。同様に、区間$k$に進入する前の物体の速度が$v_{k-1}$のとき、区間$k$を通過した直後の物体の速度$v_k$は、$v_k=\fbox{ウ}$で、区間$k$を通過するのにかかる時間$\Delta t_k$は、$\Delta t_k=\fbox{エ}$である。また、${v_k}^2-{v_{k-1}}^2=\fbox{オ}$なので、$\Delta t_k=\fbox{カ}$と表すこともできる。

$F_1=F_2=\cdots=F_n\gt 0$のとき、$1\leqq i\lt j\leqq n$であれば、$v_i\fbox{キ}v_j$なので、$\Delta t_i\fbox{ク}\Delta t_j$となる。区間$k$を通過した時の、物体の運動量と運動エネルギーの変化をそれぞれ、$\Delta P_k$、$\Delta E_k$とすると、$\Delta P_k=\fbox{ケ}$、$\Delta E_k=\fbox{コ}$と書けるので、$\Delta P_i\fbox{サ}\Delta P_j$、$\Delta E_i\fbox{シ}\Delta E_j$である。

• (1) $v_0+\dfrac{F_1\Delta x}{mv_0}$
• (2) $v_0+\dfrac{F_1}{2m}\left(\dfrac{\Delta x}{v_0}\right)^2$
• (3) $v_0+2\dfrac{F_1}{m}\Delta x$
• (4) $-\sqrt{-{v_0}^2+2\dfrac{F_1}{m}\Delta x}$
• (5) $\sqrt{{v_0}^2+2\dfrac{F_1}{m}\Delta x}$
• (6) $\Delta x+\dfrac{F_1}{2m}\left(\dfrac{\Delta x}{v_0}\right)^2$

• (1) $\dfrac{\Delta x}{v_0}$
• (2) $\sqrt{\dfrac{2m}{F_1}\Delta x}$
• (3) $\dfrac{m}{F_1}\left(-v_0+\sqrt{{v_0}^2+2\dfrac{F_1}{m}\Delta x}\right)$
• (4) $\dfrac{\Delta x}{v_1}$
• (5) $\dfrac{1}{2}\left(\dfrac{\Delta x}{v_0}\right)^2$
• (6) $\dfrac{m}{F_1}\left(v_0-\sqrt{-{v_0}^2+2\dfrac{F_1}{m}\Delta x}\right)$

• (1) $v_{k-1}+\dfrac{F_k\Delta x}{mv_{k-1}}$
• (2) $v_{k-1}+\dfrac{F_k}{2m}\left(\dfrac{\Delta x}{v_{k-1}}\right)^2$
• (3) $v_{k-1}+2\dfrac{F_k}{m}\Delta x$
• (4) $-\sqrt{-{v_{k-1}}^2+2\dfrac{F_k}{m}\Delta x}$
• (5) $\sqrt{{v_{k-1}}^2+2\dfrac{F_k}{m}\Delta x}$
• (6) $\Delta x+\dfrac{F_k}{2m}\left(\dfrac{\Delta x}{v_{k-1}}\right)^2$

• (1) $\dfrac{\Delta x}{v_{k-1}}$
• (2) $\sqrt{\dfrac{2m}{F_k}\Delta x}$
• (3) $\dfrac{m}{F_k}\left(-v_{k-1}+\sqrt{{v_{k-1}}^2+2\dfrac{F_k}{m}\Delta x}\right)$
• (4) $\dfrac{\Delta x}{v_k}$
• (5) $\dfrac{1}{2}\left(\dfrac{\Delta x}{v_{k-1}}\right)^2$
• (6) $\dfrac{m}{F_k}\left(v_{k-1}-\sqrt{-{v_{k-1}}^2+2\dfrac{F_k}{m}\Delta x}\right)$

• (1) $2\dfrac{F_k}{m}\Delta x$
• (2) $2\dfrac{m}{F_k}\Delta x$
• (3) $\dfrac{m}{2F_k}\Delta x$
• (4) $\dfrac{2}{m}$
• (5) $\dfrac{m}{2}$
• (6) $\left(\dfrac{2F_k\Delta x}{m}\right)^2$

• (1) $\dfrac{2\Delta x}{v_k+v_{k-1}}$
• (2) $\dfrac{\Delta x}{2(v_k+v_{k-1})}$
• (3) $2\left(\dfrac{\Delta x}{F_k}\right)^2\dfrac{\Delta x}{v_k+v_{k-1}}$
• (4) $\left(\dfrac{F_k}{\Delta x}\right)^2\dfrac{\Delta x}{2(v_k+v_{k-1})}$
• (5) $\dfrac{F_k\Delta x^2}{m(v_k+v_{k-1})}$
• (6) $\dfrac{F_k\Delta x^2}{2m(v_k+v_{k-1})}$

• (1) $\lt$
• (2) $=$
• (3) $\gt$

• (1) $mv_k$
• (2) $\dfrac{1}{2}m{v_k}^2$
• (3) $F_k\Delta t_k$
• (4) $(F_k-F_{k-1})\Delta t_k$
• (5) $F_k\Delta x$
• (6) $(F_k-F_{k-1})\Delta x$
• (7) $\dfrac{F_k}{m}\Delta t_k$
• (8) $\dfrac{F_k}{m}\Delta x$

• 問1 極板面積$S$、極板間隔$d$の平行平板コンデンサーがある。2枚の極板の電気量はそれぞれ$+Q$、$-Q$である。極板間の以下の量を答えなさい。ただし、極板間には一様な電界ができているとし、クーロンの法則の比例定数を$k$とする。
  • (a) 電気力線の本数$\fbox{ス}$
    $\fbox{ス}$の選択肢
    • (1) $Q$
    • (2) $4\pi Q$
    • (3) $4\pi kQ$
    • (4) $\dfrac{4\pi kQ}{d}$
    • (5) $\dfrac{4\pi kQS}{d}$
    • (6) $\dfrac{4\pi kQ}{S}$
    • (7) $\dfrac{4\pi kQd}{S}$
  • (b) 電界の強さ$\fbox{セ}$
    $\fbox{セ}$の選択肢
    • (1) $\dfrac{Q}{d}$
    • (2) $\dfrac{4\pi Q}{d}$
    • (3) $\dfrac{4\pi SQ}{d}$
    • (4) $\dfrac{4\pi kSQ}{d}$
    • (5) $\dfrac{4\pi Q}{S}$
    • (6) $\dfrac{4\pi kQ}{S}$
    • (7) $\dfrac{4\pi kQ}{Sd}$
  • (c) 電圧$\fbox{ソ}$
    $\fbox{ソ}$の選択肢
    • (1) $Qd$
    • (2) $4Qd$
    • (3) $4\pi Qd$
    • (4) $4\pi kQSd$
    • (5) $\dfrac{Qd}{S}$
    • (6) $\dfrac{4\pi kQ}{S}$
  • (d) 電気容量$\fbox{タ}$
    $\fbox{タ}$の選択肢
    • (1) $\dfrac{S}{4\pi}$
    • (2) $\dfrac{S}{4\pi d}$
    • (3) $\dfrac{S}{4\pi kd}$
    • (4) $\dfrac{kS}{d}$
    • (5) $\dfrac{Sd}{4\pi}$
    • (6) $\dfrac{4\pi kS}{d}$
    • (7) $\dfrac{kSd}{4\pi}$
• 問2 電気量$Q_1$の2個の正電荷が距離$2a$を隔てて位置$\text{A}$と位置$\text{B}$に置かれている。直線$\text{AB}$の中点から、直線に垂直に距離$b$だけ離れた位置$\text{C}$に電気量$Q_2$の正電荷を図1のように置く。クーロンの法則の比例定数を$k$として、次の問いに答えなさい。
  
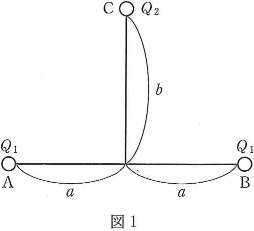
  • (a) 電気量$Q_2$の電荷に働く静電気力の大きさはいくらか。$\fbox{チ}$
    $\fbox{チ}$の選択肢
    • (1) $\dfrac{kQ_1Q_2}{\sqrt{a^2+b^2}}$
    • (2) $\dfrac{2kQ_1Q_2}{\sqrt{a^2+b^2}}$
    • (3) $\dfrac{kQ_1Q_2}{\sqrt{(a^2+b^2)^3}}$
    • (4) $\dfrac{2kQ_1Q_2}{\sqrt{(a^2+b^2)^3}}$
    • (5) $\dfrac{2kaQ_1Q_2}{\sqrt{(a^2+b^2)^3}}$
    • (6) $\dfrac{2kbQ_1Q_2}{\sqrt{(a^2+b^2)^3}}$
    • (7) $\dfrac{2kabQ_1Q_2}{\sqrt{(a^2+b^2)^3}}$
  • (b) 次に、$a=b=r$、$Q_1=Q_2=Q$とすると、位置$\text{A}$におかれた電荷に働く静電気力の大きさはいくらになるか。$\fbox{ツ}$
    $\fbox{ツ}$の選択肢
    • (1) $\dfrac{kQ^2}{4r^2}$
    • (2) $\dfrac{\sqrt{2}kQ^2}{4r^2}$
    • (3) $\dfrac{\sqrt{3}kQ^2}{4r^2}$
    • (4) $\dfrac{\sqrt{5}kQ^2}{4r^2}$
    • (5) $\dfrac{(\sqrt{2}+\sqrt{3})kQ^2}{4r^2}$
    • (6) $\dfrac{(\sqrt{2}+\sqrt{5})kQ^2}{4r^2}$
    • (7) $\dfrac{(\sqrt{3}+\sqrt{5})kQ^2}{4r^2}$
    • (8) $\dfrac{kQ^2}{4r^2}\sqrt{3+2\sqrt{2}}$
    • (9) $\dfrac{kQ^2}{4r^2}\sqrt{5+2\sqrt{2}}$
    • (0) $\dfrac{kQ^2}{4r^2}\sqrt{2+2\sqrt{3}}$
    • (+) $\dfrac{kQ^2}{4r^2}\sqrt{5+2\sqrt{3}}$
    • (-) $\dfrac{kQ^2}{4r^2}\sqrt{2+2\sqrt{5}}$
• 問3 起電力が$E_1$、$E_2$、$E_3$の3個の電池がある。
  • (a) 電池の内部抵抗を各々$r_1$、$r_2$、$r_3$とする。これらの電池を図2の様に並列につなぎ、外部抵抗$R$と接続する。外部抵抗$R$に流れる電流はいくらか。$\fbox{テ}$
    
    
    $\fbox{テ}$の選択肢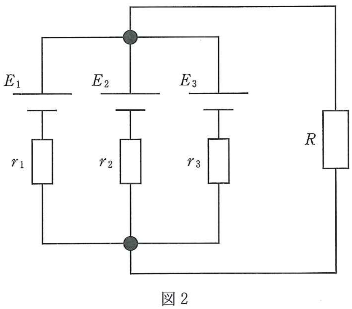
    • (1) $\dfrac{r_2r_3E_1+r_3r_1E_2+r_1r_2E_3}{(r_1r_2+r_2r_3+r_3r_1)R+r_1r_2r_3}$
    • (2) $\dfrac{(E_1+E_2+E_3)r_1r_2r_3}{({r_1}^2r_2+{r_2}^2r_3+{r_3}^2r_1+r_1r_2r_3)R}$
    • (3) $\dfrac{{r_1}^2E_1+{r_2}^2E_2+{r_3}^2E_3}{(r_1r_2+r_2r_3+r_3r_1)R+r_1r_2r_3}$
    • (4) $\dfrac{{r_2}^2r_3E_1+{r_3}^2r_1E_2+{r_1}^2r_2E_3}{({r_1}^2r_2+{r_2}^2r_3+{r_3}^2r_1+r_1r_2r_3)R}$
    • (5) $\dfrac{(E_1+E_2+E_3)r_1r_2r_3}{(r_1r_2+r_2r_3+r_3r_1)R^2}$
    • (6) $\dfrac{r_2r_3E_1+r_3r_1E_2+r_1r_2E_3}{({r_1}^2r_2+{r_2}^2r_3+{r_3}^2r_1+R^2)R}$
    • (7) $\dfrac{(E_1+E_2+E_3)r_1r_2r_3}{(r_1r_2+r_2r_3+r_3r_1)R+r_1r_2r_3}$
  • (b) 内部抵抗が互いに等しく$r_1=r_2=r_3=r$としたとき、外部抵抗$R$に流れる電流を$I_p$とする。次に、3個の電池を直列接続した場合に外部抵抗$R$に流れる電流を$I_s$とすると、両者の比$I_s/I_p$はいくらになるか。$\fbox{ト}$
    $\fbox{ト}$の選択肢
    • (1) $1$
    • (2) $\dfrac{r}{R}$
    • (3) $\dfrac{R}{r}$
    • (4) $\dfrac{3R+r}{R+3r}$
    • (5) $\dfrac{R+3r}{3R+r}$
    • (6) $\dfrac{rR+r^2}{R^2+rR}$
    • (7) $\dfrac{R^2+rR}{rR+r^2}$